前一页
回目录
新物理学——阴极射线与电子——阳极射线或原子射线——放射性——X射线与原子序数——量予论——原子结构——玻尔学说—一量子力学——相对论——相对论与万有引力——物理学近况——核型原子——化学
新物理学
十九世纪最后十年以前,物理科学一直循着第六章所叙述的发展路线前进。当时以为物理学的主要框架已经一劳永逸地构成了。以后需要做的一点点工作就只是把物理常数的测量弄得再准确一些(小数点后面的数字再推进一位),并把看起来往往很快就能解决的光以大结构的研究工作再推进一步。二十世纪的前三十年,这一牛顿的体系渗入新的物理学学说中。在解释实验的结果时,起初这一体系唯一无二的学说,后来便和其他学说并用。慢慢地才发现还需要一些全新的概念。
新物理学可以说是从1895年慕尼黑伦琴(Wilhelm KonradRontgen,1845-1923年)教授发现X射线时开始的。在这以前,已经有很多人对气体中的放电进行实验,特别是法拉第、希托夫、盖斯勒(Geissler)、戈尔茨坦(Goldstein)、克鲁克斯等人和后来的人J.汤姆生(1856-1940年),即剑桥大学三一学院的主任教授约瑟夫·汤姆生爵士。但是只有持具远见的人才觉得这些实验重要,而最先引起物理学家注意这些实验的,便是伦琴的工作。
伟大发现之出于偶然,常较一般人所想象的为少。不过伦琴找到X射线的踪迹却是偶然的,这件事的确迟早要发生,但仍然是偶然的。伦琴发现紧密封存的底片虽丝毫不暴露在光线下,如果放在高度真空的放电管附近,仍然会变灰黑而至毁坏。这说明放电管内发出某种能穿透底片封套的光线。
伦琴发现,一个涂有磷光质,如铂氰酸钾的幕屏放在这种放电管附近时,即发亮光;金属的厚片放在管与磷光屏中间时,即投射阴影,而轻的物质,如铝片或木片,平时不透光,在这种射线内投射的阴影却几乎看不见。所吸收的射线的数量似乎大致和吸收体的厚度与密度成正比。真空管内的气体愈少,则射线的贯穿性愈高。具有相当“硬度”的射线,可使肌肉内的骨骼在磷光片或照片上投下阴影。因此,在有了适当的技术之后,这一事实对于外科医术,就具有无上的价值。
从纯粹科学的观点来看,继X射线之后,J.J汤姆生等人又有一个更重要的发现:当这些射线通过气体时,它们就使气体变成导电体。在这个研究范围内,液体电解质的离子说已经指明液体中的导电现象有类似的机制。液体电解质的离子说是由法拉第创立的,后来主要由科尔劳施、范特-霍夫和阿累利乌斯加以发展。现在这个气体的离子说证明是更加成功。
在X射线通过气体以后,再加以切断,气体的导电性仍然可以维持一会儿,然后就渐渐消失了。汤姆生与卢瑟福又发现:当由于X射线射入而变成导体的气体,通过玻璃绵或两个电性相反的带电板之间时,其导电性就消失了。这说明气体之所以能导电是由于含有荷电的质点,这些荷电的质点一与玻璃绵或带电板之一相接触,就放出电荷。卢瑟福又发现:在导电的气体内,电流的强弱起初和电动势成正比;但如果电动势继续增高,则电流的增加渐渐变慢,最后达到一个最大的饱和数值。从这些实验可以明白,虽然离子是液体电解质中平常而永久的构造的一部分,但在气体中,只有X射线或其他电离剂施作用时才会产生离子。如果听其自然,离子就会渐渐重新结合而至消失。玻璃绵的表面很大,可以吸收离子或帮助离子重新结合。如果外加的电动势相当高,便可以使离子一产生出来就马上跑到电极上去,因而电动势再增高,电流也不能再加大。
伦琴的发现还开创了另一研究领域——放射现象的领域。X射线既然能对磷光质发生显著的效应,人们自然要问:这种磷光质或他种天然物体,是否也可以产生类似X射线那样的射线呢?在这一研究中首先获得成功的是亨利·柏克勒耳(Henri Becquerel)。他在1896年2月发现,钾铀的硫酸复盐发出的射线,可以穿透黑纸或其他不透光的物质,对照相底版发生影响,后来他发现铀本身与其所有化合物都有同样的作用。
次年,1897年,是以超原子微粒(即远比任何元素的原子更轻的质点)伟大发现著称的一年。物理学的新肘代从此开始了。
阴极射线与电子
当一只装有铂电极的玻璃管,经抽气机逐渐抽空时,管内的放电在性质上就经历多次变化,最后就在玻璃管壁上或管内其他固体上产生磷光效应。然后,这些物体就成为X射线的来源。1869年,希托夫证明放在阴极与玻璃壁间的障碍物,可以在玻璃壁上投射阴影。1876年,戈尔茨坦证实希托夫的结果,而创造“阴极射线”一词,他以为这种射线是和普通光线同一性质的以太波。另一方面,伐利(Varley)和克鲁克斯提出证据——例如,这些射线在磁场中发生偏转——说明它们是由阴极射出的荷电质点,因撞击而产生磷光。1890年,舒斯特(Schuster)观察了它们在磁场中的偏转度,测量了这些假想质点的电荷与其质量的比率,而估计这一比率为液体中氢离子的比值的500倍左右。他假定这些质点的大小与原子一样,推得气体离子的电荷远较液体离子为大。1892年赫兹发现阴极射线能贯穿薄的金片或铝片。这一发现,似乎与组成射线的质点为普通原子流或分子流的想法颇难调和。1895年,贝兰证明:这些质点偏转到绝缘的导电体上时,就把它们所有的负电荷给与导电体。在1897年,质点的速度及其电荷e与质量m的比值,为几个物理学家测定之后,它们的性质的问题就得到了解决。一月间,维歇特(Wiechert)证明几种射线的速度约为光速的十分之一;而其e/m则等于电解液中氢离子的比值的2000至4000倍。他按电容器的振荡周期测量速度,而按磁场中的偏转测量e/m。七月间考夫曼(Kaufmann)发表他的实验报告:他从电极间的电位差与磁场中的偏转,求得质点的能量。同时J.J汤姆生将这些射线导入绝缘的圆柱,测量其电荷,并观测其给予温差电偶的热量,而求得其动能。最后他于十月间发现在高度真空下,阴极射线不但能为磁场所偏转,也能为电场所偏转,他因而测量了这两种偏转度。
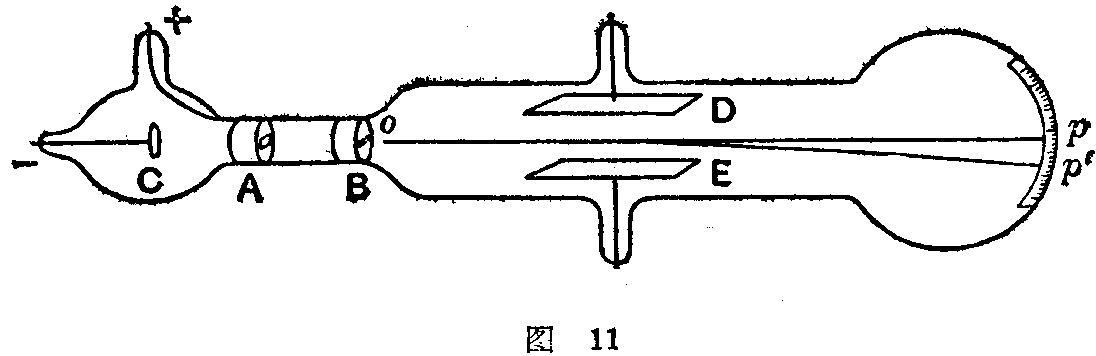
图11表明汤姆生用来进行上述有历史意义的实验的仪器。一支高度抽空的玻璃管装着两个金属电极:阴极C和开有小缝的阳极A。从C发出的阴极射线的一部分,穿过小缝后,再为第二个小缝B所削细。这样得到的小束射线,经过绝缘片D与E之间,射在玻璃管他端的荧光幕或照相底片上。如将绝缘片连于高电压电池的两极,则其间产生电场。整个仪器放在一强力的电磁体两极中间,使得射线也受到磁场的作用。
假定阴极射线是荷有负电的质点的急流,由简单计算可以看出,射线的电场偏转度,亦如其磁场偏转度,是依质点的速度v及其电荷与质量之比e/m而改变的。所以通过测量电场与磁场的偏转度,便可求得v与e/m的数值。
汤姆生求得质点的速度在光速的十分之一左右,而略有变化,但其e/m则不管气体的压力与性质及电极的性质如何,均无改变。在液体电解质中,以氢离子的e/m为最大,约为10,000或104。汤姆生求得气体离子的e/m为7.7×106,换言之,即为液体中氢离子的e/m的770倍,而考夫曼在1897年12月所求得的更精密的数值为1.77×107。这些结果也许表明,在气体内的阴极射线的质点中,不是象舒斯特所预料的那样,电荷比在氢原子中大得多,就是质量小得多。汤姆生暂时假定这些质点比原子小。他以牛顿所常用的微粒那个名词去称呼它们,并且说它们是我们寻求多年的各种元素的共同成分。但是当时还没有明确的证据可以证明这些微粒所负的电荷,不比电解质中单价离子所负的更大,因而也无法计算其质量。所以电荷的疑案就成了急待研究的下一个问题了。
1898和1899年,汤姆生测量了X射线在气体中所造成的离子的电荷。他利用威尔逊(C.T.R.Wilson)在1897年所发现的方法,即离子和尘埃一样,可以成为潮湿空气中蒸汽凝成雾滴的核心。从这些雾滴在空气阻力下降落的速度,可以计算出雾滴的大小。从凝结的水的体积,可以求得雾滴的数目,再从已知电动势所产生的电流,可以求得电荷的总量。不久以后,汤森(Townsend)测量了离子渗入气体的扩散速度,而由此计算出离子的电荷。到了1899年,汤姆生用云室法与磁场偏转法,测量了相同一种质点(以紫外光射在锌片上所产生的质点)的电荷e和e/m。所有测量结果都证明:在实验误差限度以内,气体质点的电荷与液体单价离子的电荷相符合。事实上,在米利根(Millikan)新近的实验结果中,这两个数字相差不及四千分之一。
由此可见,并非微粒的电荷比液体中氢离子的电荷更大,而是其质量更小。这些微粒是原子的一部分,无论元素的性质如何,均为其原子共有的成分。从汤姆生最初的实验来看,每一微粒的质量似约为氢原子的1/770。但从上述考夫曼测量的e/m,已可求得较精密的结果。自此以后关于微粒的电荷与其e/m,接着又有新的测定,最著名的是米利根的测定。他在1910年改进威尔逊的云室法,又在1911年测量了小油滴在被电离的空气中降落的速度。当一油滴捉到一离子时,其速度便忽然改变。这样求得离子的电荷为4.775×10-10静电单位。这说明这些微粒或电子的质量,为氢原子的1/1830。从气体分子运动论可求得一个氢原子的质量约为1.66×10-24克,所以一个电子的质量约为9×10-28克。
这个伟大的发现终于解决了一个古希腊留下的问题:即不同的物质是否有共同的基础的问题。同时也阐明了“带电”的意义。汤姆生当时发表其个人的观点说:
我认为一个原子含有许多更小的个体;我把这些个体叫做微粒。这些微粒彼此相等;其质量等于低压下气体中阴离子的质量,约为3×10-28克。在正常原子中;这些微粒的集团,构成一个中性的电的体系。个别的微粒,行为虽然好象阴性的离子,但聚集于中性的原子中时,其阴电效应便为某种东西所抵消。此种东西使微粒散布的空间,好象有与这些微粒电荷之和相等的阳电似的。气体的带电现象,我认为是由于气体原子的分裂,致使微粒脱离某些原子。脱离出来的微粒,性质如阴性的离子,每个都荷有一值量的阴电,为简便计,我们名之为单位电荷。剩余的原子的另一部分,性质如一阳性的离子,载有一单位的正电荷,还有比阴电子更大的质量。由此观之,带电现象主要是由于原子的分裂,其中一部分质量被放出,而脱离了原来的原子。
这些新发展与前不久的一种研究,颇有关联之处。按照麦克斯韦的理论,光既然是一种电磁波系,那么光必定是由振荡的电体所发出的。由于光谱是元素所特有的而不是元素的化合物所特有的,所以这些振荡体(或称振子)必为原子或原子的一部分。依照这种推理,洛仑兹(Lorentz)在汤姆生的发现的前几年,创立了一种物质的电学说。这个学说预料,光谱的出现当受磁场的影响,而这一预料已为塞曼(Zeeman)所证实。塞曼在1896年发现光源放
在强磁场之内时,其所发纳光谱的谱线即行变宽。他后来又以更强的磁场将单一谱线分成了两条或多条。根据测量这些线条之间的距离所得的资料,按照洛仑兹的学说,可以算出振荡质点的电荷与其质量之比e/m的新值。如是求得此值的数量级为107电磁单位,根据更精密的测量算出,此数字为1.77×107,与根据观察阴极射线和他法所得的结果甚为符合。
洛仑兹利用斯托尼(J.Stoney)所定的名称“电子”来称呼这些振动的带电质点,而塞曼效应的发现与测量证明,它们就是汤姆生的微粒。我们可以把它们当做是孤立的阴电单位。拉摩(Larmor)以为电子既然有电能,就必定有与质量相当的惯量。这样,洛仑兹的学说就成为物质的电子学说,而且和由汤姆生发现而来的观点完全融合在一起。只不过汤姆生是用物质去解释电,而洛仓兹却是用电来解释物质。
应该指出,当时还有一个默认的假设并没有为后来的研究所证实。这一假设认为,原子中的微粒或电子是按照牛顿的动力学运动的,在最初的时候,人们甚至把原子比做一个小型的太阳系,电子在其中的运动有如行星之绕太阳。但在1930年以前,我们明白这种行星轨道的概念,并不一定符合事实,因而应该放弃。
接着人们便发现还可以用许多别的方法获得微粒或电子:例如高温下的物质及受到紫外光作用的金属,都能发出电子。这些效应由勒纳德(Lenard)、埃尔斯特(Elster)和盖特尔(Geitel)、理查森(O.W.Richardson)、拉登堡(Ladenburg)等人加以研究,此后这种热效应在无线电报与电话所用的热离子管中就取得了重要的实用意义。
阳极射线或原子射线
由上所述,阴极射线是在真空管放电时,自阴极射出的。其对应的、自阳极发出的阳射线,是戈尔茨坦在1886年发现的。观察阳射线的方法是在阳极对面的阴极上穿些小孔,这样在放电时,便有发光的射线经过这些孔,人可以在阴极以外去观察它。维恩(Wien)和汤姆生在1898年先后测量了这种“极隧射线”的磁偏转与电偏转。其e/m的数值表明这种阳射线是由质量与普通原子或分子相近的阳性质点所组成的。
汤姆生在1910年和1911年把阳射线的研究推进了一步。他利用一个高度抽空的大仪器,在阴极装上一个长而细的导管,这样便带到一个很细的射线束,其位置可以在仪器内的照相底片上加以记录。妥善安排磁力与电力,使二者所生的偏转互成直角。由于磁偏转与质点的速度成反比,而电偏转与其速度的平方成反比,如果射线中有速度不同的同类质点,则照片上将呈现抛物线形的曲线。但实际出现的曲线则视仪器中残存气体的性质而定。如气体为氢,则基本曲线所给与的e/m为104或m/e为10-4,与液体电解质中氢离子的数值相等。第二条曲线所给出的值为前者的两倍,即表明有一种氢分子,其质量二倍于负有一个单位的电荷的氢原子的质量。其他元素给出多条抛物线组成的复杂体系。每个元素的m/e 与氢原子的m/e之比,汤姆生称之为“电原子量”。
汤姆生考察氖元素(原子量为20.2)时,发现两条曲线,一条表示原子量为20,另一条表示原子量为22。这说明,普通制备的氖气可能是两种化学性相同而原子量不同的元素的混合物。某些放射现象也说明有这种元素,并且可以给予解释,索迪(Soddy)把它们叫做“同位素”(希腊文τσοτοποs,即在周期表中占同一位置之意)。
汤姆生的实验由阿斯顿(Aston,1877-1945年)加以继续和发展。他用改进的仪器,求得各元素的有规律的“质谱”。这样就证实氛有同位素。氯的原子量为什么是35.46,也是化学家长久所不了解的,至此也证明氯是原子量为35与37的两种氯原子的混合物了。阿斯顿于他种元素也得到相似的结果。如果将氧的原子量定为16,则其他所有已经测验过的元素的原子量,都非常接近整数,差别最大的是氢的原子量,它不是1,而是1.008。这些原子量所以与整数有微小差别,是由于原子核中阴阳二单位体密积在一起的缘故。这个问题还要在后面详细讨论。
这样,阿斯顿就澄清了另一老问题。纽兰兹与门得列耶夫的工作,证明各元素不同的性质与其原子量的陆续增加有某种关系,因而不可避免地说明原子量自身应当形成一个简单顺增的序列。普劳特关于各元素的原子量都是氢原子量的倍数的假说,至此证明接近真实。至于其中的稀微差异,在现代原子论中,既可予以解释,也饶有趣味。
放射性
在柏克勒耳对于铀的放射性质进行了创始的观察以后,跟着便发现铀的射线亦如X射线,能使空气和他种气体产生导电性。钍的化合物也经人发现有类似的性质。1900年,居里(Curie)夫妇进行了有系统的研究,在各种元素与其化合物以及天然物中寻找这种效应。他们发现沥青铀矿与其他几种含铀的矿物,比铀元素本身更为活跃。他们采用化学方法,即按其放射性分离了沥青铀矿的成分。于是三种很活跃的物质,即镭、钋与锕的盐就由几位学者分离出来。其中最活跃的是镭,是居里夫妇与贝蒙特(Bemont)合作而发现的。沥青铀矿中镭的含量极微,许多吨的矿,经过漫长而繁重的工作,仅能分离出一克的极小分数的镭盐。
1899年,蒙特利尔(Montreal)的卢瑟福教授,即以后的剑桥大学教授卢瑟福爵士,发现铀的辐射里有两部分,一部分不能贯穿比1/50毫米更厚的铝片,另一部分则能贯穿约半毫米的铝片,然后,强度就减少一半。前者,卢瑟福叫做α射线,能产生最显著的电效应;而贯穿性较大的一部分叫β射线,能通过不漏光的遮幕,而使照相底片变质。以后又发现第三种更富贯穿性的辐射,称为γ射线,在贯穿一厘米厚的铅片之后,还能照相,并使验电器放电。镭放射所有这三种射线比轴容易得多,与其一般活动性成比例,所以研究这些辐射,也以用镭最为便利。
贯穿性中等的γ射线,容易为磁铁所偏转,而柏克勒耳还发现它们也为电场所偏转。柏克勒耳确凿地证明它们是射出的荷电质点。进一步的研究,证明β射线在一切方面都象阴极射线,虽然其速度约为光速的60至95%,但比已经试验过的任何阴极射线的速度都大,所以B射线就是阴性的微粒或电子。
强度足够使B射线产生相当大的偏转的磁场和电场,并不足以影响很容易被吸收的a射线。虽然在1900年前后,人们已经认为α射线很可能是荷阳电的质点,其质量较组成阴性B射线的质点的质量大,但在若干时期以后,才由实验证明它也能为磁场和电场所偏转,但其方向与β射线偏转的方向相反而已。卢瑟福在1906年对于α射线进行实验,求得其e/m为5.1×103。电解波中氢离子的e/M为104。因为已有证据(见后)表明,α射线是氨的组成物,由此可知α质点是荷有二倍于单价离子的电荷的氦原子(原子量为4)。它们的速度约为光速的1/10。
贯穿性最强的Y射线,不能为磁力或电力所偏转。它们与其他两种射线不是同类的,而和X射线相似,由一种与光同性质的波所组成,其波长经康普顿(A·H.Compton)、埃利斯(C.D.Ellis)与迈特纳(Fraulein Meitner)等测量,远比光波为小。它们似乎也象某些X射线一样,含有发射体所特有的各种单色成分。
1900年,威廉·克鲁克斯爵士发现,如果以碳酸氨使铀自其溶液中沉淀,而再溶其沉淀物于过量的试剂中,则所余留的为少量不浓的渣滓。这点渣滓克鲁克斯称为铀-X以照相法试验,异常活动,但再溶解的铀,则无照相效应。柏克勒耳也得到相似的结果:他发现活动的渣滓如果搁置一年,则丧失其活动性,而不活动的铀反恢复其固有的辐射性。
1902年,卢瑟福与索迪发现铁也有相同的效应,即在为氨所沉淀时,钍的活动性,即消失其一部分。滤液蒸干,则产生放射性极强的渣滓。但经过一月,渣滓的活动性丧失,让则恢复其原有的活动性。这种活性的渣滓,钍-X,证明是另外一种化学物质,因为它只能为氨全部分开,别种试剂虽能使钍沉淀,但不能使它与钍-X分离。因此当时断定这些X化合物(未知的化合物)当是另外的个体,不断地由母体发出,而渐渐丧失其活性。
1899年,卢瑟福发现从钍发出的辐射变异无常,尤其易为吹过放射物质表面的空气缓流所影响。他认为这种效应是由于有一种物质放射出的缘故,这种物质的性质好象一种有暂时放射性的重气体。这就是当时所谓的“射气”。这种射气必须与上述以高速度依直线进行的辐射明显分开。射气慢慢地弥散到大气里去,好象挥发性液体的蒸气一般。它的作用象是直行辐射的独立源泉,但随时间的进展,其活动性就变得衰弱起来。镭和锕发出相似的射气,但铀和钍则否。镭射气和氖与氩相似,是一种惰性气体,现在叫做氡。
放射物质所发出的射气为量极小。1904年,拉姆赛与索迪从几分克溴化镭得到一个很小的射气泡。在一般情形下,其量之微,远不足以影响抽空器内的压力;除利用其放射性侦察它之外,也不能用其他方法去侦察它。普通所得到的,是它与大量空气的混合物,只能和空气同时从一器输入他器。
1899年,居里夫妇发现如将一棒暴露在镭射气里,则棒自身也获得放射性质。同年,卢瑟福于钍也得着相同的结果,而且进行了详细的研究。如果将棒自盛有射气的器内取出,而塞入检验简内,则此棒可使简内的气体电离。如将暴露于钍射气而得到放射性的铂丝,用硝酸洗涤,铂丝的放射性不受损失。可是如果用硫酸或盐酸洗涤,其放射性就差不多全部丧失。将酸蒸干则得含有放射性的渣滓。这些结果,表明铂丝的放射性是由于积有某种新的放射物的缘故,这种放射物与各种化学试剂有其一定的反应。这种新的放射物当是它由之形成的那种射气分裂的产物。
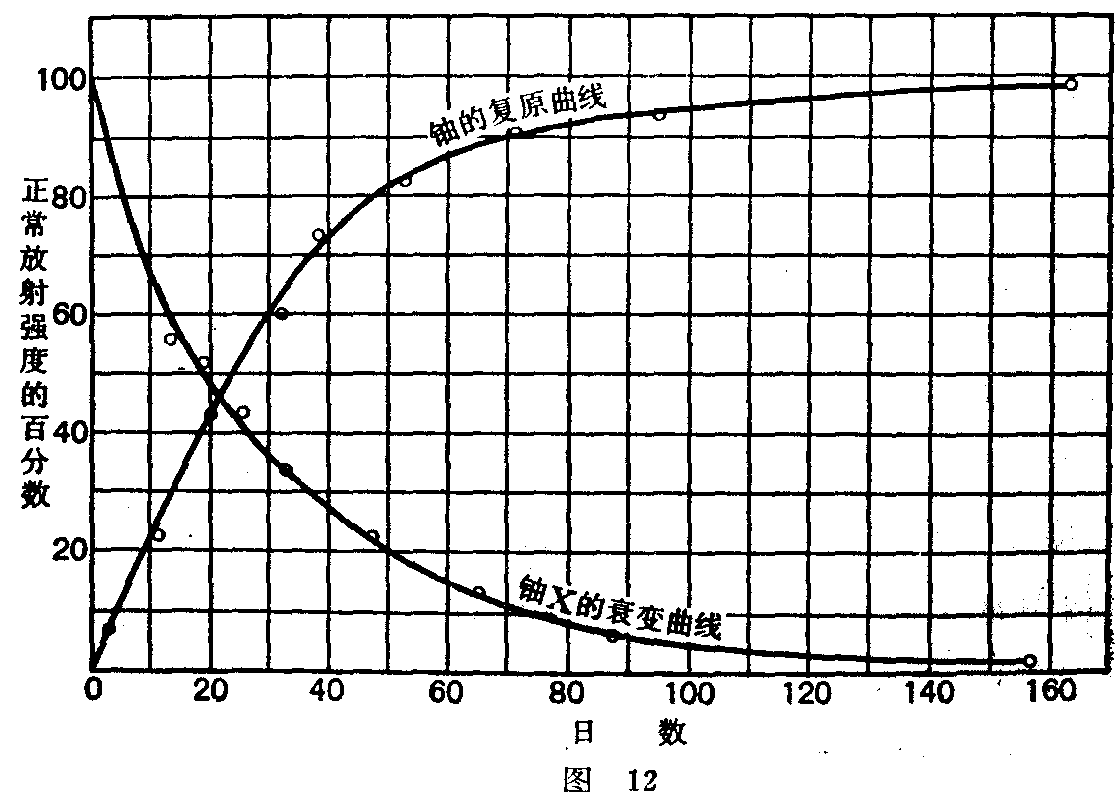
卢瑟福与索迪在1902年研究了钍-X放射性的衰变率,而获得重要的发现;即在每一段短时间内的变率与这段时间开始时的放射物的强度成比例。铀-X也有类似的现象。其过程有如图12所示。这与化合物按每个分子分解为比较简单的物体时,在量上的减少遵循同一定律。但当两个或多个分子互相反应引起化学变化时,两者的定律便不相同了(见245页)。
1903年,居里与拉波尔德(Laborde)注意到一个奇特的事实:镭的化合物不断地发热。他们从实验的结果算出每克纯镭每小时可发热约100卡。以后的结果证明一克镭与其产物平衡时,每小时发热135卡。这种热能的发出率,不论将镭盐放在高温或液体空气的低温下,都不改变,甚至在液体氢的温度下也不至减小。
卢瑟福认为热能的发射与放射性有关。丧失了射气的镭,如以电的方法测量,其放射性的恢复与其发热本领的恢复保持同一速率,而其分离出来的射气发热量的变化,也与其放射性的变化相应。放射物的电效应主要是由于a射线。而其热效应也主要决定于α质点的发射。在上述的每小时135卡中,只有5卡来自β射线,6卡来自γ辐射。α与β射线的热效应显然得自射出质点的动能。
由于发现镭的化合物不断发热,人们进行了许多探索,力求解释这个好像永不枯竭的能量的泉源,人们的注意力也集中于放射问题本身。
需要解释的事实可以总结为以下几点:(1)什么时候有放射性即有化学变化出现,什么时候就有新体出现;(2)这种化学变化是单质点的分离,而不是化合;(3)放射性与放射元素(不论其是独立的或化合的)的质量成比例,因此分离的质点不是分子而是原子;(4)其所放出的能量是已知的最猛烈的化学反应的万千倍。
1903年,卢瑟福与索迪根据他们对于射气与其遗留的放射物的实验结果,提出一个学说来解释所有已知的事实。这个学说就是:放射性是基本原子的爆炸分裂造成的。在数百万个原子中,这里和那里忽然有一个爆裂,射出一个α质点,或一个β质点和一个γ射线,所遗留下来的部分就成为另一不同的原子。如果射出的是一个α质点,这个新原素的原子量将有所减少,减少的数值是一个氦原子的原子量的四个单位。
现在把最初制订的镭族的系谱列表于下(根据最近的研究,这个系谱已经有所不同)。这个系谱从铀开始,这是一个重元素,原子量为238,原子序数为92,这个数字,以后还要说明,是原子外部的电子数。镭族系谱列如下表:
| 铀Ⅰ | 92 | 238 | 14.5×109年 | α |
| 铀X1 | 90 | 234 | 24.5日 | β,γ |
| 铀X2 | 91 | 234 | 1.14分 | β,γ |
| 铀Ⅱ | 92 | 234 | 106年 | α |
| 锾 | 90 | 230 | 7.6×104 | α |
| 镭 | 88 | 226 | 1600年 | α |
| 镭射气 | 86 | 222 | 3.82日 | α |
| 镭A | 84 | 218 | 3.05分 | α |
| 镭B | 82 | 214 | 26.8分 | β,γ |
| 镭C | 83 | 214 | 19.7分 | α,β,γ |
| 镭C’ | 84 | 214 | 10-6秒 | α |
| 镭D | 82 | 210 | 25年 | β,γ |
| 镭E | 83 | 210 | 5日 | β,γ |
| 镭F(钋) | 84 | 210 | 136日 | α |
| 铅 | 821 | 206 | 无放射性 |
铀原子放射一个a质点,即一个质量为4而阳电荷为2的氦原子后,所遗下的是一个轴X1原子,其原子量为238-4=234,而原子序数为92-2=90。铀X1所放射的仅仅是β与γ射线。β射线的质量很小,载有一个阴电荷,所以,由铀X1变来的所谓铀X2,较铀X1少一阴电荷,换言之即多一阳电荷,因此其原子序数为91,其原子量实际没有什么变化,仍为234。铀X3也只放射β与γ射线,所以其子体铀Ⅱ的原子序数为92,而原子量仍为234。
这样照表中所示类推。在放出α射线时,产物的原子量减少4位,其原子序数少2单位。如果放出的是β射线,则重量几无改变,而其原子序数则增加1单位。
镭族的最后已知子体为铅,其原子量经理查兹(Richards)与赫尼格斯密特(Honigschmit)测定为206,而普通铅的原子量为207。钍族的最后产物也证明为铅,其原子量经索迪测定为208。阿斯顿还测定锕铅的原子量有正常的数值207,在铀族里还有一种具有放射性的铅,以镭D的身分出现,其原子量为210。这四种铅具有相同的化学性质,因而可以认为是同位素。
原子学说,虽然由道尔顿的化学工作确立起来,但是百余年来一直不能证明有单个原子存在;我们只能按成万成亿的数目对原子作统计式的处理。而今,利用放射性,我们已经能够探索单个a质点的效应了。克鲁克斯将硫化锌的荧光幕暴露在一个溴化镭小点之下,用放大镜观察到幕上的闪烁。这是最初的办法,今天已经有其他的侦察方法了。
如果我们用比激发火花所必需的强度稍弱的电场对几毫米水银柱压力下的气体施加作用,这种气体就进入非常灵敏的状态。一个α质点,因为速度极大会因为与气体分子碰撞,而产生成千上万的离子。这些离子,受到强电场的作用,也作急速的运动,通过碰撞而更产生其他离子。这样,一个α质点的总效应就成倍地增加可以使灵敏静电计的指针在标尺上有20毫米或更大的偏转。卢瑟福用一个极薄的放射物质膜,使指针的转动减少到每分钟三、四次,而数计所发射的α质点的数目,由此可以估算出镭的寿命。计算表明,镭的质量在1600年中减少一半。
另一方法是威尔逊发明的。当a质点射过为水蒸气所饱和的空气时,α质点所产生的离子就形成水蒸气凝结的核心。因此空气中呈现雾的路径,代表每个α质点的行程,而这些雾的路径,是可用照相方法去记录的。
卢瑟福关于放射性的研究,最后指明了物质嬗变的可能性——中世纪点金术士的梦想。不过,一直要到后来,才发现了加速这些变化的人为方法,特别是控制这些变化的人为方法。这些变化的发生完全决定于原子内部的偶然情况,而变化发生的频率也符合熟悉的概率的定律。但在1919年,卢瑟福发现用a射线进行撞击时可以引起几种元素(如氮)的原子的变化。氮的原子量为14,其原子为三个氦核(共重12)与两个氢核所组成。在受到a质点撞击时,氦核就被击破,氮原子组成成分中的氢核就以高速射出。在这里我们第一次看到用人力随意分裂原子(单向嬗变)的可能性,此后,这种方法又有很大的扩大。可是破坏易而建设难:这不等于说我们能够用轻而简单的原子造出重而复杂的原子。当时,有证据表明,复杂的放射性原子发放出能量来,因此,人们起初以为物质的演化历程是单向的:即由复杂原子分裂为简单原子与辐射能。但是以后的研究证明,虽然重原子分裂时发出能量,而轻原子形成时也能发出能量(见后391,422页)。X射线与原子序数
伦琴所发现的X射线,既不象普通光那样折射,也找不到什么有规律的反射与偏振的痕迹;但是,另一方向,X射线也不象阴极射线或a及B质点那样可以为磁场或电场所偏转。因此X射线的性质一度成为大家讨论的问题。到1912年,劳厄(Laue)方提出一项意见,认为如果X射线是彼长很短的以太波,则晶体中各原子有规则的排列就可以使X射线发生衍射,正像刻有许多平行线痕的平面可以当作光栅使用来使普通光衍射一样。劳厄求出其繁复的数学理论,弗里德里希(Friedrich)与基平在实验中成功地证实了这种理论。于是人们才知道X射线是比光波更短的电磁波,而这一发现,也就开辟了一个研究晶体结构的新天地。最先探勘这个新天地的主要是威廉·布拉格(William Bragg)和他的儿子劳伦斯(Lawrence)·布拉格。他们利用岩盐(简单的正六面形晶体),用这种衍射现象证明,与岩盐天然晶面平行的原子面间的距离为2.81×10-8厘米,而用阴极射线撞击钯靶时所发生的特有的X射线的波长为0.570×1010-8厘米,仅合钠光波长的万分之一。这样,人们所知道的辐射的波长就包括了很大范围,从无线电通信的长波,一直到X射线和Y射线的短波,中间大约有60个倍频程(每一个倍频程是频率增加一倍的频率范围)。其中可见光大约仅占一个倍频程。
威廉·布拉格爵士、莫斯利、C.G.达尔文和凯(Kaye)的工作证明,把晶体当作光栅所产生的X射线的衍射光谱,是由一定限度内一切波长的漫射辐射混合组成的,并且包括作为“谱线”叠于光谱之上的某些更强烈的一定频率的辐射。这些具有特征的线辐射是一种同利用可见光所得的线光谱相似的衍射现象。随着这一现象的发现,牛津大学一位青年学者莫斯利在1913和1914年又有一个非常重要的发现。他不久就死于欧战。这是物理科学界的一个莫大的损失。
莫斯利将阴极射线所撞击的靶,从一种金属换成另一种金属,并且以亚铁氰化钾晶体作为光栅,对每一金属靶所生的X射线的光谱加以考察,发现光谱中具有特征的谱线的振荡频率,由于改换金属,而发生简单的改变。如果以n代表X射线光谱中最强谱线每秒钟振荡次数,则按照周期表从一个元素到下一个元素,n的平方根增加的数目都是相等的。如果将n[1/2]乘一常数,使这种有规则的增加成为单位,我们就得到一系列的原子序数。在这个序列中,所有已经测量过的固体元素的原子序数,都排列得很有规律,从铝的13到金的79。如果再把其他已知的元素填入,我们就发现,从氢的1到铀的92,中间只有两三个空位代表尚未发现的元素。这几个元素后来也发现了(见426页)。
| 原子序数 | 元素 | 符号 | 原子量 | 原子序数 | 元素 | 符号 | 原子量 |
| 1 | 氢 | H | 1.0080 | 14 | 硅 | Si | 28.086 |
| 2 | 氦 | He | 4.00260 | 15 | 磷 | P | 30.9738 |
| 3 | 锂 | Li | 6.941 | 16 | 硫 | S | 32.06 |
| 4 | 铍 | Be | 9.01218 | 17 | 氯 | Cl | 35.453 |
| 5 | 硼 | B | 10.81 | 18 | 氩 | A | 39.948 |
| 6 | 碳 | C | 12.011 | 19 | 钾 | K | 39.102 |
| 7 | 氮 | N | 14.00067 | 20 | 钙 | Ca | 40.08 |
| 8 | 氧 | O | 15.994 | 21 | 钪 | Sc | 44.9559 |
| 9 | 氟 | F | 18.9984 | 22 | 钛 | Ti | 47.90 |
| 10 | 氖 | Ne | 20.179 | 23 | 钒 | V | 50.9414 |
| 11 | 钠 | Na | 22.9898 | 24 | 铬 | Cr | 51.996 |
| 12 | 镁 | Mg | 24.305 | 25 | 锰 | Mn | 54.9380 |
| 13 | 铝 | Al | 26.9815 | 26 | 铁 | Fe | 55.847 |
| 27 | 钴 | Co | 58.9332 | 60 | 钕 | Nd | 144.24 |
| 28 | 镍 | Ni | 58.71 | 61 | 钷 | Pm | 145 |
| 29 | 铜 | Cu | 63.545 | 62 | 钐 | Sm | 150.4 |
| 30 | 锌 | Zn | 65.37 | 63 | 铕 | Eu | 151.96 |
| 31 | 镓 | Ga | 69.72 | 64 | 钆 | Gd | 157.25 |
| 32 | 锗 | Ge | 72.59 | 65 | 铽 | Tb | 158.9254 |
| 33 | 砷 | As | 74.9216 | 66 | 镝 | Dy | 162.50 |
| 34 | 硒 | Se | 78.96 | 67 | 钬 | Ho | 164.9303 |
| 35 | 溴 | Br | 79.904 | 68 | 铒 | Er | 167.26 |
| 36 | 氪 | Kr | 83.80 | 69 | 铥 | Tm | 168.9342 |
| 37 | 铷 | Rb | 85.4678 | 70 | 镱 | Yb | 173.04 |
| 38 | 锶 | Sr | 87.62 | 71 | 镥 | Lu | 174.97 |
| 39 | 钇 | Y | 88.9059 | 72 | 铪 | Hf | 178.49 |
| 40 | 锆 | Zr | 91.22 | 73 | 钽 | Ta | 180.9479 |
| 41 | 铌 | Nb | 92.9064 | 74 | 钨 | W | 183.85 |
| 42 | 钼 | Mo | 95.94 | 75 | 铼 | Re | 186.2 |
| 43 | 锝 | Tc | 98.9062 | 76 | 锇 | Os | 190.2 |
| 44 | 钌 | Ru | 101.07 | 77 | 铱 | Ir | 192.22 |
| 45 | 铑 | Rh | 102.9055 | 78 | 铂 | Pt | 195.09 |
| 46 | 钯 | Pd | 106.4 | 79 | 金 | Au | 196.9665 |
| 47 | 银 | Ag | 107.868 | 80 | 汞 | Hg | 200.59 |
| 48 | 镉 | Cd | 112.40 | 81 | 铊 | Tl | 204.37 |
| 49 | 铟 | In | 114.82 | 82 | 铅 | Pb | 207.2 |
| 50 | 锡 | Sn | 118.69 | 83 | 铋 | Bi | 208.9806 |
| 51 | 锑 | Sb | 121.75 | 84 | 钋 | Po | 209 |
| 52 | 碲 | Te | 127.60 | 85 | 砹 | At | 210 |
| 53 | 碘 | I | 126.9045 | 86 | 氡 | Rn | 222 |
| 54 | 氙 | Xe | 131.30 | 87 | 钫 | Fr | 223 |
| 55 | 铯 | Cs | 132.9055 | 88 | 镭 | Ra | 226.0254 |
| 56 | 钡 | Ba | 137.34 | 89 | 锕 | Ac | 227 |
| 57 | 镧 | La | 138.9055 | 90 | 钍 | Th | 232.0381 |
| 58 | 铈 | Ce | 140.12 | 91 | 镤 | Pa | 231.0359 |
| 59 | 镨 | Pr | 140.9077 | 92 | 铀 | U | 238.029 |
量子论
1923年康普顿发现,当X射线为物质所散射时,波的频率变小。他用辐射的光子单元理论,来解释这个效应。这种光子单元可以和物质或电荷的电子与质子相比。电子在原子轨道中运动自然不免发放辐射能量。按照牛顿动力学,这个效应将使其轨道缩小,从而使其转动周期变短,使其发射的频率增高。在这个过程的所有阶段中,都会有原子存在,所以在一切光谱里都应该可以发现一切频率的辐射,而不是我们在许多元素的线状光谱中所看到的少数确定不变的频率的辐射。
就是在白炽固体的连续光谱内,能量也不是均匀分布的,而是在某些频率之间为最强。这个最强辐射的区域随温度增高,在光谱里由红端至紫端移动。这些事实很难用原子或电子辐射的旧理论去解释。事实上,数学的计算表明频率高的振子应该比频率低的振子发出更多的能量;因此,可见光比不可见的红外线应该发出较多的热,而紫外线又应该比可见光所发的更多。但是这一切都是与众所周知的事实相反。
为了解决这些困难,1901年普兰克提出了“量子论”,主张辐射不是连续的,而象物质一样,只能按个别的单元体或原子来处理。这些单元的吸收与发射,服从在物理学与物理化学的其他分支中早已广泛地使用的概率原理。辐射出来的能量,其单元大小并不是一样的,而与其振荡频率成正比。所以只有当拥有大量可用的能量的时候,振子才能拥有和发射出高频率的紫外线;因为振于拥有许多这样的单元的机会很小,所以其发射的机会和发射的总能量也都很小。反之,频率低的辐射是以小单元射出的,振子拥有许多小单元的机会较多,因而其发射的机会也可以较多;但由于其单元甚小,其总能量也甚小。只有在某段适中的频率范围内,单元的大小适中。机会也好,于是发出的单元数目可以相当大、而其总能量便得达到其最高值。
为了解释这些事实,必须假设普兰克的能量子e与频率成正比,或者说与振荡周期成反比。因此我们可以写成
E=hv=h/T,
式中v表频率,T表振荡周期,而h是一常数。因此,普兰克常数h等于能量与时间的乘积。ET,这个量被称为作用量。这个守恒的作用单位,当然不随频率而改变,事实上是不随任何变化的东西而改变。这是一个真正的自然单位,和从电子中求得的物质和电的自然单位类似。
我们可以把一种专为解释某一系列事实而创立的理论加以调整,使其与那些事实相适合,但不论怎样适合,以及其形式怎样新颖,这个理论可以普遍适用的证据也许并不充分。可是,如果有另一套完全不同的现象,也可以用同一的理论去解释,尤其是在这些现象没有别的合理的解释的时候,这种证据的价值必大为增高,而我们也就开始相信,我们可以依赖这个理论去解释更多的关系。
普兰克的理论本来是为了解释辐射的事实而创立的。因为与传统的动力学有抵触,所以一般学者虽非怀疑,也以审慎的态度对待,亦属当然。但当其为爱因斯坦、条恩斯特与林德曼(Lindemann),特别是德拜(Debye)用以解释比热现象之后,它广泛应用的可能性便大为增加了。
普通的分子运动论以为,固体中单原子分子的原子热,应为气体常数的3倍,或约为每度6卡,而且此数不受温度的影响。金属都含有单原子分子,其原子热在普通温度下大致不变,等于6。但在低温下,则此数值便减小了。
解释这个现象首先获得成功的是爱因斯坦。他指出,如果能量只能以一定的单元或量子而被吸收,则吸收的速率必随单元的大小而改变,因而必随振荡的频率与温度而改变。德拜从量子论推出一个与实验符合的公式,特别显著的例子是碳元素,其原子热即使在普通温度下,也随温度而改变,比较金属的数值小得多。
依照量子论,光在发射与吸收的刹那间,即不是弗雷内尔的稳定以太波,也不是麦克斯韦与赫兹的连续电磁波。它好象是一团一团的微量的能量所组成的流;这些细团的能量几乎可以看做是光的原子,虽与牛顿的微粒不同类,而却与之相当。这个现象与干涉现象的协调是留待将来解决的难题。如果将一线光分为两道,而使其经过长短不同的路程,则这二路程虽相差至数千个波长,但在这两道光的最后会合处,也可见干涉的条纹。又在大望远镜里看见的星像的衍射花样,表明每个原子所发的光都充满着整个物镜。以前,人们认为这些事实足以证明光是以稳定的“波列”前进的,均匀地分布于几千个波长的距离之内,而且在横向上扩展,足以充满望远镜全部空间。
可是,如果使这颗星的光线落在钾的薄膜上,则被星光所发出的电子,每个都有与该星光相当的量子的能量。这里,光的行动不象是波,而象是能量集中的枪弹。距离增大,则一定面积上所受到的枪弹必减少,但是枪弹冲击的动量还是相等。另外一个现象即X射线使气体发生电离,也是光的旧理论难于解释的。如果波阵面是均匀的,它对于其行程上所遇到的分子应发生相同的效应,但实际上每百万个分子当中或者只有一个被电离。有许多理由说明,这大概不是由于不稳固的分子太少。J.J.汤姆生等人说这现象是由于X射线与光并不按宽的波阵面,而只沿局部的以太丝(法拉第的力管)前进的缘故。
接着,量子论又表示光在另一方面也不是连续的。为了解释全部事实和调和互相矛盾的观点,汤姆生设想“光是由质点组成的,每一质点为一闭合的电力圈,并伴有一列的波”。德布罗意引用新近的概念建立一个理论,将波的性质和微粒的性质联系起来,而成立一种新型的“波动力学”。一个运动的质点的性能像一个波群,其速度v与波长入和质点的速度u及其质量m的关系为λ=h/mv,式内h为普兰克常数。波的速度为c2/v,式内c为光的速度,而u为质点与波群的速度。于是我们不能不注意到这些现代的光的理论与牛顿想像的微粒和波的综合体很相似。
原子结构
现代的原子理论开始于1897年,当时发现各元素都有阴电微粒,并且查明这些微粒即是电子。这一发现,也说明原子之所以有电的性质是由于其所含电子多于或少于电子的正常数目,而其光学性质则可以解释为电子的振荡。
勒纳德早期的观察表明,阴极射线能通过真空管内铝窗而至管外。根据这种观察,他在1903年以吸收的实验证明高速的阴极射线能通过数千个原子。按照当时盛行的半唯物主义者的看法,原子的大部分体积是空无所有的空间,而刚性物质大约仅为其全部的10-9(即十万万分之一)。勒纳德设想“刚性物质”是散处于原子内部空间里的若干阳电和阴电的合成体。
这个关于必需的阳电荷的说法不能使人满意,于是J.J.汤姆生又进行了更有系统的尝试来描绘原子结构。
汤姆生以为原子含有一个均匀的阳电球,若干阴性电子在这个球体内运行。他按照迈耶尔(Alfred Mayer)关于浮置磁体平衡的研究证明,如果电子的数目不超过某一限度,则这些运行的电子所成的一个环必能稳定。如果电子的数目超过这一限度,则将列成两环,如此类捱以至多环。这样,电子的增多就造成了结构上呈周期的相似性,而门得列耶夫周期表中物理性质和化学性质的重复再现,或许也可得着解释了。
但是1911年盖格(Geige)和马斯登(Marsden)关于α射线撞击物质时形成散射的实验,使卢瑟福对于原子的性质采取另外一种看法。α质点的雾迹通常多是直线的,有时也有突然改变其方向的。阴电子加于α质点上的力势必很小,不能造成这种散射。但如果假定原子为空格结构的复杂体,含有一个凝聚为小核的阳电荷,而阴电子在原子内的空处围绕着核转动,则上述的效应便可得着解释。由于正常原子是中性的,所以,核里的阳电荷,必与所有电子的电荷之和量相等而性相反。而且由于电子的质量远远小于原子的质量,所以原子的质量几乎全部凝聚于原子核。
这一理论形成时,人们把原子看做是一个太阳系,把质重的核比拟为处于中心的太阳,而质轻的电子则类似绕核运转的行星。长冈(Nagaoka)于1904年研究了类似系统的稳定性,但首先用实验证据去支持这个看法的是卢瑟福。勒纳德关于阴极射线的吸收的研究与后来其他的实验表明,如果将原子比拟为以电子为行星的小太阳系,则原子内的空间,照比例说也必定象太阳系里的空间那么大。在这个行星式的电子理论中,牛顿物理学给予我们的先入之见,或许引导我们走得太远了,以至超过事实所能保证的境界,但是,就阴极射线与放射质点的贯穿性而论,原子确是一个很空松的结构。
一个运动的电荷带着一个电磁力场。由于它有能量,因而也必有惯性。所以一个电荷具有一个类似质量的东西,也许就具有我们所谓物质的基本成分的本质。如果以电荷为中心,画一小球以代表电子,则与这球外的力场相联系的有电磁质量。J.J.汤姆生据数学分析表明,除非电荷以极大速度运行,其电性质量为2e2/3r,式内e为电荷,r为其半径。因此,如果假定所有的电磁能量都在电子之外,则根据已知的质量与电荷值,便可计算出其半径。这样算得电子的半径为10[-18]厘米。如果假定半径r很小,换言之,如果将电荷浓聚,则某有效质量也增大(参看下面所说的新的研究)。与电子相当的阳性单元,即氢的原子核,叫做“质子”。它的质量,基本上等于原子的质量,即阴电子的质量的1800倍。因此,如果假定所有质量都是有电性的,而原子核是围绕着一个点状阳电荷的球,则原子核的半径就仅是电子半径的1/1800,或约为5×10-17厘米。但须在此申明,这些估计是根据一项关于电荷分布的武断假定。现在,这些估计的价值已经很可疑了。
这些概念在当时虽有帮助,而现在已经经过修改。但是我们仍须假定氢原子是由一个单位的阳电核和其外围的一个阴电子所组成的。氨的原子核为四个质子及两个与之紧联的电子所组成。因为氢的原子量为1.008,而氦的原子量,如阿斯顿所测量的,为4.002,所以这个复核的形成,意味着一份质量的消失:4×1.008-4.002=0.03及与之相当的能量的发射。重原子的放射性分裂,放出能量。因此我们认为一切原子部储有能量,当其分裂之时,例如铀的原子分裂时,都能释放能量。但是这里的推论又表明,氦还原为氢要吸收能量——要使氦核分裂就必须做功。看来,轻的原子核形成时放出能量,而重的原子核分裂时也放出能量。这就可以解释:为什么重的原子核有放射性,为什么自然界没有比铀更重的原子存在:它太不稳固了。由于a射线是飞行的氨原子群,所以,氦原子大概是组成其他较重原子的一部分材料。氦原子本身虽是四个质子或氢核所组成,但其结合很牢固,即使在a质点的冒险生涯中,也不能使它分离。所以其他原子大概是若干阳电单位(大概是氦核,有时还带有氢质子)与若干数目较少的阴电子结成的复核所组成的。因为核内的电子的数目较少,核上呈现纯净阳电荷的数目n,即等于莫斯利的原子序数。其余的电子存在于核心的外围。因为在中性原子内,这些外围电子所荷的阴电的总和必须与核内的纯净的阳电中和,所以n也代表原子外围电子的总数。
因为原子可被电离,而且依其化学价,可获得一、二、三甚至四个单位的电荷,所以可以在一个原子中加入或减去少数电子,而使其性质无根本的改变。我们可以假设这些电子位于原子的外围,别的电子在其内圈,更有些电子则成为原子核的必要的部分,而且一般是其稳固的部分。
以上说过,多数放射变化发射a质点。而a质点又是质量为4的氦原子,带有两单位的阳电荷。所以这种变化是原子核的崩溃变化。变化后的剩余物质量较原有的少四单位,而且变化时放出两个阴性电子,以恢复其中性状态:结果便成为一个新原子与新元素了。
玻尔学说
哥本哈根的玻尔(N.Bohr)于1913年在曼彻斯特的卢瑟福实验室工作时,首先将普兰克的量子论应用于原子结构的问题。他的工作是以当时物理学家所公认的行星式电子论为根据的。
当时已经知道:如果我们所考虑的不是光谱中通常的谱线波长,而是其在一厘米中的波数,则氢的复杂光谱呈现若干规律。当时发现,所谓“振荡数”可以用两个项的差数表示。第一项以发现者得名,叫做里德堡常数,即每厘米109,678个波。
这些关系完全是从经验得来的,最初是靠揣测,最后才求得一项符合于实验结果的算术规则。但是玻尔却根据量子论提出了解释。他指出:如果“作用量”只能以单位的整倍数被吸收,则在电子可以运行的全部轨道中,只有某些个是可能的。在最小的轨道上,作用量为一个单位或h,在第二轨道上,作用量为2h,如此类推。
玻尔假设氢原子的一个电子有四个可能的稳定轨道,相当于以单位数递增的作用量,如图13所表示的那样。图中的圆圈表示这四个稳定轨道,而其半径表示电子从一个轨道跳至另一个轨道可能的六种跃迁。这里,玻尔抛弃了牛顿的动力学,而值得注意的是平方反比律仍可应用于假设围绕原子核运行的电子,但是这些轨道本身又表现十分新奇的关系。一个行星可以在无穷多个轨道当中的任何一个轨道上围绕太阳运动,其实际的轨道为其速度所决定。可是,玻尔假定一个电子只能在几个轨道当中的一个轨道上运动。它如果离开一个轨道必须立刻、好象不经过二轨道间的空间那样,跳到另一轨道上去。由这个假设得出的理论上的结果,与通过实验所确立的关于振荡数的经验规则相当符合。还可从这里计算出常数R的绝对值为每厘米109,800波,与上面所说的最近测定的里德堡常数之值异常符合。在这一阶段,玻尔学说表现有其长远而成功的前途。
辐射的各种不同的类型可以归因于原子结构的各不同部分。X射线的光谱大都不受温度或原子的化合状态的影响。而可见光与红外及紫外光的光谱则与这两者有关。放射现象,上面说过,是原子核的爆裂造成的。现今所得的数据表明X射线起源于原子核外的内层电子,而可见光与红外及紫外线则来自最外层的电子;这些外层电子比较容易脱离,因而是和凝聚力与化学作用有关系的。
假设一个或多个电子同时存在于互相化合的二原子内,则可给化合作用以很好的解释。但如果围绕原子核而转动的电子理论来表示这种结合,则未免困难,因此在1916至1921年间,有人,特别是科塞尔(Kossel)、刘易斯(Lewis)与兰格缪尔试图创造静止的原子模型。这种模型对于原子价与化学性质的解释是成功的,但要想阐明光谱则不得不创设牵强附会的假设了。无论如何,当时的物理学家总是偏向于玻尔的动力的原子模型的。
无论采取哪一种原子模型,电离电位的事实,确是能级的基本观念的有力的证据。1902年勒纳德首先证明,电子经过气体时,必具有一定最低限度的能量,才足以产生电离。这最低的能量可以用电子为了获得其速度所必须降落的电位的伏特数来量度。最近实验的结果,如弗兰克(Franck)与赫兹关于汞蒸气的实验(1916-1925),证明当电位达到某一定伏特的倍数时,电离便达到某些明确的极大值。同时气体的光谱也发生了变化。例如弗兰克与赫兹证明,具有4.9伏特所产生的速度的电子使低压的汞蒸气发出具有一条明线的光谱。可以设想,这条谱线相当于玻尔原子内电子从第一外层回到其正常状态的跃迁。自那时以后,正象玻尔学说所预期的,已经发现许多“临界电位”,同突然出现的若干条或若干群谱线相当。萨哈(Saha)、罗素(Russell)、福勒(Fowler)、米尔恩(Milne)等研究了温度与压力对于光谱的影响。他们用热力学的方法应用了这些新概念。所得结果在天体物理学上有很大重要性,而且在恒星温度的测量方面揭开了新的一页。
图13所表示的圆形轨道,仅是氢原子的一个初浅的模型。玻尔与索末菲(Sommerfeld)都证明椭圆轨道也可产生同样的系线光谱。他们也研究了其他更为复杂的原子系统,但数学上的困难很大,因为互相吸引的三体的运动不能以有限的项数来表达。
关于玻尔原子的文献很多,进展也很不少。其结果与光谱的粗略结构大体相合,很足以使人相信这个学说在正确的途径上前进。但是这个学说虽然能说明氢和电离氦的线状光谱,却不能解释中性氦的原子光谱的精细结构,以及其他重原子的复杂结构。谱线的数目与电子从一能级到另一能级的可能跃迁数,不再相符。于是一时极为成功的玻尔原子学说渐露破绽,到1925年就显然逐渐破产了。
量子力学
玻尔的原子模型,把电子比拟为运转的行星。这个模型远离观察到的事实,超出万无一失的范围。对于原子,我们只能从外面进行考察,观察进去的与出来的东西,如辐射或放射质点等。玻尔所描绘的是至少可以产生原子的某些性质的一种机制。但是别的机制或许也可以产生同样的作用。如果我们只见时钟的外面,我们可以想象有一套推动时钟指针的齿轮,使指针的转动与我们所看见的相同。但是别人也可想象有另一套齿轮,与我们所想象的一样有效。二者孰是孰非,无人可以断言。此外,仅仅研究一个体系中热量与能量的变化的热力学,也并不能利用原子观念所描绘的内部机制的图象。
1925年,海森堡只根据可以观察到的事实,即原子所吸收或发射的辐射,创立了量子力学的新理论。我们不能指定一个电子某一时刻在空间中所占的位置,或追寻它在轨道上的行踪,因而我们无权假设波尔的行星式轨道的确是存在的。可以观察到的基本数量是所发出的辐射的频率与振幅以及原子系统的能级。这些数量正是这个新理论的数学公式的依据。这一理论已经由海森堡、玻恩(Born)和约尔丹(Jordan)迅速加以推进,并从另一观点由狄拉克(Dirac)迅速加以推进,而且证明,从这一理论可以推出巴尔默关于氢光谱的公式,以及观察所得的电场与磁场对这一光谱的效应。
1926年,薛定谔从另一个角度来解决这个问题。他发挥了德布罗意关于相波与光量子的研究成果,根据“质点由波动体系组成,或者说只不过是波动体系而已”的观点,导出另外一个理论。这个理论,在数学上实与海森堡的理论等价。他以为,运载这种波的介质具有散射性,如透明物质之于光,或高空电离层之于无线电波(413页)一样。所以周期愈短,速度愈大,而两种频率不同的波有同时共存的可能。
正如在水中一样,一个单独的波的速度与波群或浪的速度并不相同。薛定谔发现:计算两个频率组成的波群的运动的数学方程式,与具有相当动能与位能的质点的通常的运动方程式相同。由此可知,波群或浪在我们面前表现为质点,而频率则表现为能量。这就立刻导致最初出现在普兰克常数h中的能量与频率的不变关系。
两个振荡很快、以至不能看见的波,可以因为相互干涉,而产生表现为光的一些“拍”,正如两个音调相差不远的声晋,可以产生音调比任何一个都低的拍一样。在含有一质子与一电子的氢原子里,波一定依照方程式的规定而存在。而薛定谔发现,只有在确定的频率,即与观察到的谱线相同的频率的情况下,这些方程式才有解。遇到较复杂的原子,玻尔学说本来已经失去效用,薛定谔却还能求得频率的正确数目,以解释光谱的现象。
如果薛定谔的波群中的一个很小,则无疑地可以指出表现这个波群的电子的地位。但随着群的扩大,电子可在波群之内任何地方,因此位置便有某些不确定。这些原理在1927年由海森堡加以推广,后来又由玻尔加以推广。他们发现:愈是想把质点的位置测定得精密些,则其速度或动量的测定将愈不精密;反之,愈是想把质点的速度或动量测定得精密些,则其位置的测定将愈不精密。总之,我们对于位置的必然不确定度与对于动量的不确定度相乘,无论如何近似地等于量子常数h。要同时确定两者的想法,似乎在自然界中找不到对应的东西。爱丁顿将这一结果叫做测不准原理,并且认为这一原理与相对论有同等的重要性。
新量子力学在习惯于革命的物理科学中又掀起了革命。海森堡、薛定谔和其他学者的数学公式是等价的。我们如果满足于这些数学方程式,对于这个理论便会有相当的信心。但是这些方程式所根据的观念,以及某些人给与它们的解释,却根本互不相同。我们很难说这些观念与解释可以维持很久,不过表现这些观念和解释的数学却是一个永久的收获。
古典力学已经成为量子力学的极限情况。古典力学之所以不能解释原子结构,是由于波长与原子的大小相近,正象当光束的宽度,或其行程中所遇的障碍物的大小与波长相近时,几何光学中所说的直线光束,也就失却其意义一样。即使在这时,要把量子力学与古典动力学与麦克斯韦的电磁方程式以及与万有引力的相对论联合起来,似乎也有可能。如果能够把知识作这样广泛的综合,这种理论将成为自然科学中有历史意义的伟大综合之一。
薛定谔的理论必须联系电子的实验来考虑。这些实验,如德布罗意的理论所表示的,证明一个运动的电子伴随有一系列的波。汤姆生的微粒。起初被看做是漫无结构的质点,继后被认为是电子,一个阴电的简单单位,不管这具有什么意义。但到了1923年和1927年,戴维森(Davisson)与耿斯曼(Kunsman)以及戴维森与革末(Germer,当时在美国工作)先后使运动缓慢的电子自晶体的表面反射,而发现它们具有波动系统的衍射性质。同年稍后,J.J.汤姆生爵士的儿子乔治·汤姆生以一电子束通过一个异常之薄的,比最薄的金箔还薄的金属片。我们知道,质点流会在薄片后面的底片上产生一块模糊的影家,但波长与薄片厚度相近的波,会产生明暗相间的圆环,与光线通过薄玻璃或肥皂膜所产生的衍射花样相似。事实上,乔治·汤姆生所得到的确是这种圆环。这说明,运动的电子伴有一列的波,这些波的波长仅是可见光的波长的百万分之一,而与有相当贯穿力的X射线的波长相近。
根据理论,如果电子伴有一列的波,则电子必须和这些波作协调的振动。因此,电子也必有它的结构,它也绝不再是物质的成电的最小单位了,即令在实验中也应该是这样。于是人们开始想象还有更小的部分。数学的研究表明,电子的能量与波的频率成正比,而电子的动量与波长的乘积为一常数。由于原子中仅有某些波长与频率,所以,电子的动量也只能有某些数值,并且不是连续地增加,而只能突跃地增加。这个非连续性的表现使我们又回复到量子论。
要解释乔治·汤姆生的实验,就需要假定电子具有双重性质:既是质点(或电荷),又是波列。上面说过,薛定谔走得更远,而认为电子是一种波的系统。波的性质是不确定的。波必须符合某些方程式,但可能不具有机械式的运动。而这些方程式可能只符合概率的交替,这一项在正常波里,度量位移量,可以给出电子出现在某一给定点的概率(机遇)。
于是在原子被分为电子之后三分之一个世纪,电子又被分为一未知的辐射源或一无形体的波动系统了。昔日的坚硬而有质量的质点的最后一点痕迹已经消失,物理学的基本概念似乎已经归结为数学方程式了。实验物理学家,特别是英国人,对于这种抽象概念很是感觉不安,企图设计一种原子模型,而从机械或电的角度去表达这些方程式的意义。但牛顿早已见到,力学的最后基础绝不是机械的。
相对论
光线传播需要时间,是丹麦天文学家勒麦(Olaus Romer)在1676年发现的。勒麦发现木星的一个卫星两次被食之间所经历的时间,在地球背木星而行时较长,在地球向木星而行时较短。他由此估计光速为每秒192,000英里。
五十年后,英国皇室天文学家布莱德雷从恒星的光行差求得与此一致的结果。从地球轨道面上的远星看地球,好象每年左右摆动一次,在相继的两个半年中,它的摆动方向是相反的。如果这颗星射出的光线击中地球,那么这条光线的瞄准方向必须在地球的前面少许,正如射击飞鸟必须瞄准飞鸟的前面一样。所以,如果星光现在射到地球真正位置的右边,则六个月以后便会射到它的左边。这意味着:我们在不同的时季所看见的远星射来的光线,不是互相平行的,在一年内看见虽好象在空间往返运动。从这个表面的运动,可以计算光速与地球在其轨道运行的速度之比。
斐索(Fizeau)在1849年首先对光经过地球上的短距离的速度作了测量。他将一束光通过齿轮上两齿间的凹处,再于三、四英里之外,用反光镜将光反射回来。如果齿轮不移动,则反射回来的光束通过轮上的同一凹处,可在对面看到。但如果将齿轮急速转动并调节其速度,则最后可找到一个速度,使射回的光束恰被下一个齿轮所遮住。齿轮旋转这个小角度所需的时间,显然即是光束往返于齿轮与反光镜之间所经历的时间。
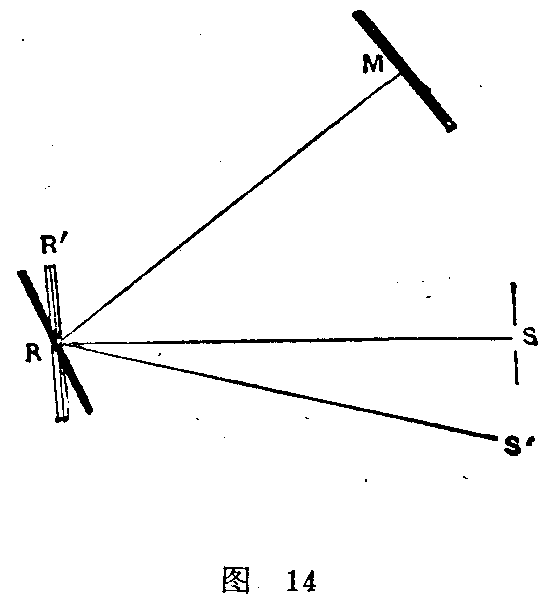
弗种设计了一个更好的方法。使从S缝(图14)射出的光束略成会聚的形式,然后在平面镜R上反射,而聚焦于凹面镜M上。这束光由M循原点射回。如果R是静止的,则S缝的影象将形成于S缝的本身上。然后以已知的速度使R急速转动,当光线往返于RM的距离时,R镜已经转过了一个小的角度,因此光的回程RS’与RS不复叠合,而转动了二倍于R镜所转的角度。于是测量SS’间的距离,便可计算光往返于RM间所需的时间。
光速最新的测量结果,比从前测量的稍小,即在真空内,为每秒186,300英里或2.998×1010厘米,或在1/1000的误差内取为3×1010厘米。
如果的确有光以太那样性质的东西,那么由于它对于通过它的光要产生影响,显然应该可以测定其运动。如果地球在以太中运动,而不扰动它,则地球与以太之间必有相对运动。那么光随以太顺行时,其速度必较其反以太逆行时为大;而总计起来,它往返横过以太流时,也当较其一次顺流、一次逆流时为大。好象游泳一样,往返对岸一次,必较顺流、逆流同游相等距离的情形为速。
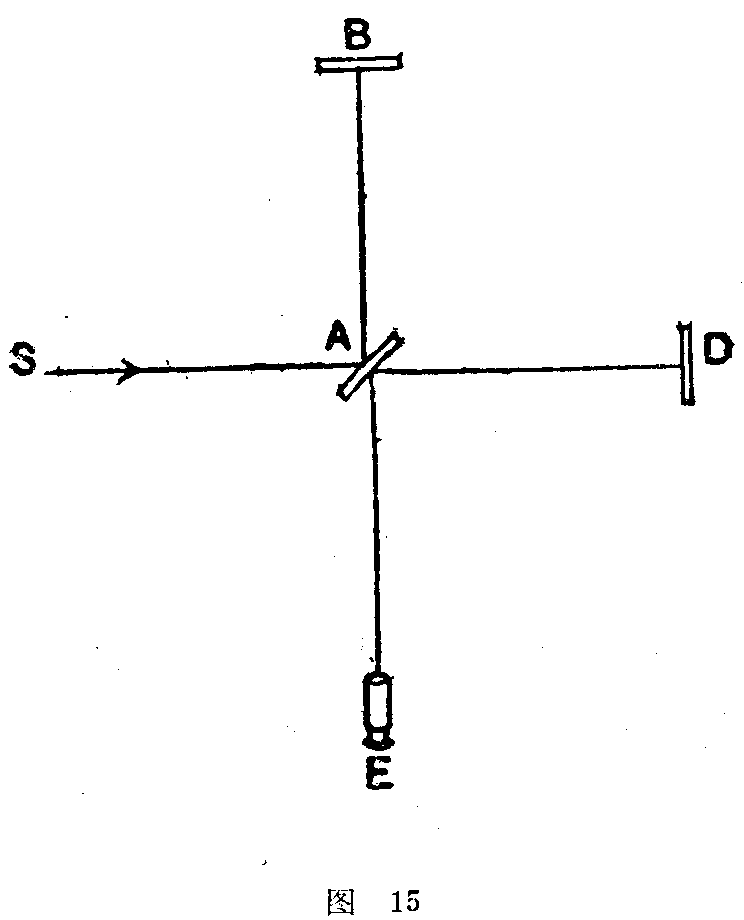
这就是迈克尔逊(Michelson)和莫利(Morley)在1887年所作的有名实验的要点。他们将一块石头浮于水银之内,然后将仪器装置在石头上面,以防振动。光束SA(图比)行至玻璃片A时,一部分为其所反射,一部分透射过去。这两部分光在B和D处又为B与D两镜所反射。如果AB=AD,则两道光的行程也相等,而在E处的望远镜内必可察见有干涉效应。今若没想地球朝SAD方向运动,而不拖曳以太同行,那么以太将流过实验室,也如风之流过树林,于是将使光经过ABA与ADA两行程的时间发生差异,而所得的干涉条纹,将和以太相对静止时不在同一位置。今若将这仪器转过一个直角,则AB成为运动的方向,而AD和它垂直,这时,干涉条纹应向相反方向移动。移动的总量为以上所说的两倍。
但是迈克尔逊和莫利并没有观察到干涉条纹有可以度量的移动,于是断定地球与以太之间并无可以察觉的相对运动。重复做这个实验的结果表明,在他们的假设下,这种相对运动,必然小于地球在其轨道上的速度的十分之一。地球好象拖曳着以太同行。
可是在以先行差计算光速时,我们假设以太不被地球在以太中的运动所扰动。而且洛治1893年在两个以(或超过)最大安全速度转动的重钢版之间,测量光的速度,也未发现光速有任何改变。由此可见,质量这样大的东西并不拖着其附近的以太同行。那末光行差的理论和从洛治实验中得出的推断,似乎又和迈克尔逊及莫利的实验结果完全不一致了。
当我们得到这样相反的结果时,如果我们还相信自然的统一性,使我们就可以断定:我们的实验和我们对于起作用的原因的看法,总有一个发生了错谬;一个富有兴趣而且必需的观念上的革命就在我们的眼前,只看我们能否领悟。
解决这个矛盾的第一个有用的看法是菲茨杰拉德(G.F.Fitz-Gerald)提出来的,又经过拉摩与洛仑兹加以发展。如果物质在根本上是带电的,或者物质的确是靠电力结合在一起的,那么,物质在带有电磁性的以太中运动时,在其运动的方向上或有收缩的可能。这种收缩除上述的现象之外,别无他法观察;一则因为效应太小,再则因为我们用以测量的尺度本身也受同样的收缩,因而在其运动的方向上,长度的单位也变短了。所以迈克尔逊与莫利的仪器,于转变方向后,也变更其大小,以至与地球经过以太时所产生的干涉条纹的移动相抵消了。
这种必需的收缩是容易计算的。物体在以太流的运动方向上将按(l-u2/c2)1/2均告的比例收缩,式中u为物体和以太的相对速度,c为不变的光速。
地球在其轨道上的速度为光速的万分之一。如果在一年的某时这是它经过以太的速度,则迈克尔逊与莫利的仪器于转动一直角时将收缩二万万分之一,这种微量的改变足以解释他们的结果。
这个问题停顿在这里若干年。无论其原因何在,所有测量光速的企图,不管是以太流顺行或逆行,都得到相同的结果,即测得的速度没有可以觉察的改变。
1905年,爱因斯坦教授对于这问题,从另外一个完全新颖的方向加以考虑。他指出:绝对空间与绝对时间的概念是想象中的虚构,一种形而上学的概念,而不是直接由物理学的观察和实验得来的。我们经验所能及的唯一空间,是用尺度上二刻度间的距离所规定的长度标准来测量的,唯一时间是用天文现象所规定的时钟来测量的。如果我们的标准也发生了菲茨杰拉德收缩这样的变化,这种变化是我们觉察不到的,因为我们和这些标准一道前进,也发生相同变化,但是,以不同方式运动的观察者却是可以觉察到这种变化的。所以时间与空间,不是绝对的,而只是与观察者相对的。
这样看来,用任何仪器、在任何情况下测量,所得的光速总是一样的事实,便不须解释了。必须承认,这个结果是新物理学第一次发现的定律。这样,可知由于时间与空间的性质,相对于任何观察者,光总是以所测得的相同的速度进行。
这个测定的速度总是一样的,但是我们对空间、时间与质量作个别测量时,不论是时间、空间或质量都没有表现出我们习惯于预期的那种但常不变性。迈克尔逊与莫利的仪器,用我们不变的标准(光速)对它加以检验,在转动时并不表现长度上有变化。这是由于我们跟随着它运动。但是,如果在枪弹飞过时,我们能足够准确地测量其长度,我们应发现它较静止时为短,而且它的速度愈近光速,它的长度也就愈短。
这个实验很难实行,但用相对性原理很容易证明:射弹的质量对于静止的观测者表现增大,而且依照长度缩短的比例而增大。设mo为低速时的质量,则高速u时的质量为mo/[1-u2/c2],式内c为光速。因此速度达到光速时,质量为无穷大。质量的改变可以用实验证明。测定以近于光速的速度经过我们身边的射弹的质量,是现代科学的奇迹之一。爆裂的放射原子所射出的B质点,可以使其经过电场与磁场,而测量其速度与质量,象测量阴极射线质点的速度和质量时一样。假设以速度不大的B质点的质量为1,则下表第二行为:根据相对论计算的、速度近于光速的B质点的质量,第三行为考夫曼根据实验测量所得的B质点的质量:
质量与缓行质点质量之比
| 质点的速度每秒厘米数 |
|
|
| 计算值 | 实值 | |
| 2.36×1010 | 1.65 | 1.5 |
| 2.48×1010 | 1.83 | 1.66 |
| 2.59×1010 | 2.04 | 2.0 |
| 2.72×1010 | 2.43 | 2.42 |
| 2.85×1010 | 3.09 | 3.1 |
B质点为阴性的电子,运动时等于电流。所以它们能产生具有能量与惯性的电磁力场。J.J.汤姆生与西尔(G.F.C.Searle)按照这个推理的路线,计算过质量随速度增加的数值,得到了相同的结果。所以质量的增加,象菲茨杰拉德的收缩一样,是与电磁理论相符合的。
而且根据相对性原理,质量与能量是等价的。一份质量m,若以能量表之,则为mc2,这里c是光速。这也是与麦克斯韦的电磁波理论相符合的。按照这个理论,电磁波具有的动量等于E/c,这里E表示它们的能量。而动量为mc,于是我们便又提出E=mc2了。
由此可见,这些原理引出了新奇意外的结果。如果我们在飞机(或以太机)内,能以近于光速的速度飞行,则我们在运动方向上的长度,据地上观测者的测量,似已缩短,我们的质量似已增大,而我们的时计也较一般的变慢。但是我们自己并不觉察有这些变化。我们的尺子或已收缩,但是我们和我们四周的一切均已收缩,所以我们不觉其变化。我们的法码或已增加质量,但我们也是一样地增加了。我们的时钟或许走得较慢,可是我们脑里的原子也运动得慢了,所以并不知时钟走慢了。
但是,因为运动是相对的,地上的观测者也正以我们对他运动的相等速度,对我们运动。所以我们对他加以测量时,便会发现他的尺度、质量与时间,也对我们表现变化,正如我们的这些量对他表现变化一样。自我们看来他好象在运动的方向上,产生了畸形的收缩,具有与其身体不相称的质量,而在身心方面迟钝得可笑;同时他对我们也有同样的观感。双方都不觉得自己的缺陷,而对于对方的悲惨变化却看得很清楚。
我们不能说两方的观测者哪一个是错误的。的确,双方都是对的。长度、质量与时间并非绝对的量。它们真正的物理数值,就是由测量所表示的。它们对双方不一样这一事实说明,它们的意义只能相对于某一观测者而规定。绝对长度、绝对空间、绝对时间或甚至时间流动的观念都是形而上学的概念,远远超过观测或实验所表示或证明的。
虽然如此,如柏格森(Bergson)所指出,在哲学的意义上,对于一个随着某系统运动或在某系统内运动的人来说,所度过的那段时间,即用以测量这个系统中的事件的时间,具有其特殊的、独一无二的重要性。但是在物理的意义上,时间与空间,单个来考虑,则是随观测者的位置而定的相对的量。不过,明可夫斯基(MinkoWski)于1968年指出,时间与空间的变化互相补偿,因此,这两者的结合,就是在这新世界里对于所有的观测者也都是一样的。我们惯于想象的空间,有长、宽、高三维,而明可夫斯基指示,我们必须把时间看做是“时空结合体”里的第四维,一秒钟相当于186,000英里,即光在这时间内所行的距离。正如欧几里得几何的连续空间中,两点的距离,无论如何测量都不变更一样,在这新的时-空连续区里,两个“事件”之间可以说有一个包括时间与空间的“间隔”,这间隔无论何人测量,都有它真正绝对的数值。我们觉得在这个变化不定的世界中,在这里找到了一种稳固的东西,因而想在这个相对性的王国内去寻求其他能保持其绝对性的量。在我们已知的量里,我们认为下面几个仍属绝对的量:数,热力学的熵,以及作用(作为量子的能量与时间的乘积)。
在空间与时间互不相干的旧世界里,人们习惯于把三度空间的整体看做是同时随着时间过去的。世界的过去和将来之间,好象隔着一个“现在的平面”,这个平面在同一刹那间伸展至空间的全部。但自1676年勒麦发现光以有限的速度进行以后,人们必定认识到,同时出现的星星实际上存在于不同的过去时间(现其不同的距离而定),至今才同时为人所看见;这样“同时”的意义便消失了。昔人信念中的绝利的“此时”变成仅仅是相对的“所见的此时”了。
科学中最近的发展已增强了相对性的观念。假设一位以光速旅行的人,游历星球,而在一年以后重返地球。在我们看来,在他飞行对,其质量好象大至无穷,而其脑筋的反应慢至无穷。我们觉得长了一岁,而他则以为时间毫未过去,他还停留在我们去年的“此时”。由此可知,认为过去与未来为一平面所划分,这个平面对于所有地区和所有人类都一样,这一类概念必须摈弃。必须从爱丁顿所谓的“此地-此时”(here-now)的一点,在空间绘出几条“所见的此时”(seen-now)线,与时轴(time-axis)成一角度,而这个角的正切等于光速。在这样绘出的三维面(类似于二维的一对锥形或滴漏形的曲面)内任何一处,我们可以找到一个绝对过去与绝对未来。在此以外,事物可以在任何观测者都觉得是不同的时间中同时存在。将过去和未来分开的劈形中立区可以叫做绝对的现在或绝对的地处,视我们从时间的角度还是从空间的角度去看它。
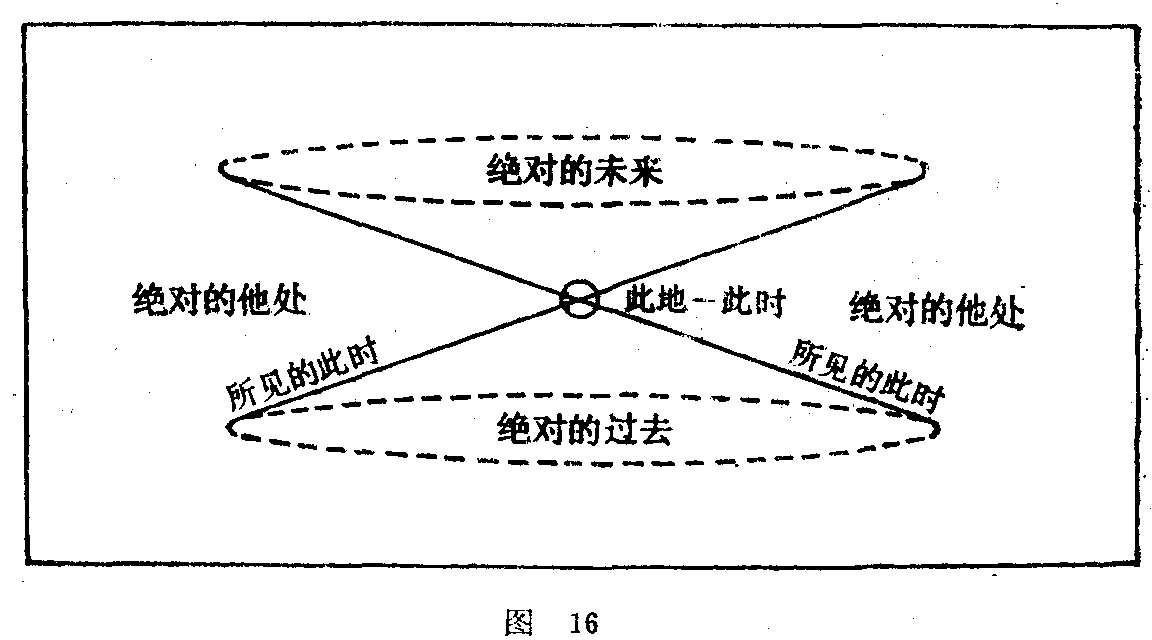
我们凭直觉意识到的时间自过去到未来的流动,在可逆的物理学中,是没有对应的。普通动力学系统(无论其为地上的或天文的)的运动方程式,从正反两个方向去了解都一样;我们不能从牛顿的公式说明行星朝哪一方向围绕太阳运行。
但是,在热力学第二定律和孤立系统中熵循一个方向向极大值增加的例子里,我们可以找到一个只能向一方进行的物理过程。因为互相冲撞而形成的分子的无规律散射,只能使这些分子接近于误差律所规定的分配速度。除非我们召唤麦克斯韦的“魔鬼”把各个分子控制起来,或守候长久的时期,以待分子因巧遇而联合成群,否则,只有赖时间的倒流才能使这个混杂的过程逆转。如果我们看见速度相等的分子逐渐类聚成群,我们可断言时间在倒流。热力学第二定律,熵增大的原则,说明一个重要无比的自然过程,相当于人类意识中时间一去不回头的前进。
相对论与万有引力
1894年,都柏林的菲茨杰拉德说:“重力可能是由于物质的存在使以太结构发生变化所致。”这句用旧物理学的语言说出的话,表达了爱因斯坦1915年把广义相对论应用于万有引力所得的结果。他证明空间的性质,尤其是光的传播现象表明,除非是在无穷小的区域内,明可夫斯基的时-空连续区和黎曼的空间相似,而不是和欧几里得的空间相似。
在这种时-空里,有些天然路线,同三维空间里,我们所惯于想象的,物体不受外力作用时所走的直线一样。既然抛射体向地球坠落,行星围绕太阳运行,可见这些路线靠近物体时即发生弯曲。因此,在物质的附近,必定有某种类似“时-空曲率”的东西存在。另一物体进入这弯曲的区域时,即循一条一定的路线走向或环绕这团物质而运行。的确,当我们从质量的角度而不是从电的角度去着想时,现今所谓物质的意义,不过是有这种曲率存在的时-空区域而已。如果我们阻止这第二物体的自由行动,如借椅子或地面的分子的冲撞使其停止的话,我们就是对它施力,但这物体却觉得这是由于它自身的“重量”所造成的。
这种效应容易用电梯加以说明。当电梯开始上升时,它受到一个加速度。这加速度在乘客看来,好象是其体重的暂时增加;增加之量,的确象普通重量一样,可用弹簧秤去衡量的。加速度的效应与所谓万有引力场中的暂时增加的效应完全相同,而且现在还不可能用我们已知的任何实验方法把这两个原因区别开来。
不过,如果现在让这电梯自由坠落,乘客将不会感觉他们在运动。如果有一乘客释放其手中的苹果,它不会比电梯坠落得更快,而仍将留在乘客身旁。这个首次把相对论运用于万有引力的“等价原理”,是爱因斯坦在1911年提出来的,数学上的困难是几年以后才得到解决的。
由此可见,牛顿关于万有引力的假设可以是不需要的。物体向地球坠落或围绕地球而运行,也许只是跟着它在时-空弯曲区域内的自然路径运行而已。
计算表明,这个理论的推论与牛顿的理论大致相同,——就一般观测的精确度而言,大体上是一样的。但是,对于一两个现象,却可以设计一种决定性的实验。其中最有名的一个是光线为太阳所偏折的观测。根据爱因斯坦的理论,算出的这种偏折度是根据牛顿的理论算出的二倍。观测这种微小偏折的唯一方法,是在日全食时拍照太阳圆面附近的星象。1919年日全食时,爱丁顿、克罗姆林(Crommelin)分别在几内亚湾的普林西比岛和巴西两处进行了这一观测。结果表明接近太阳的星象,同远离太阳的星象相比,有所移动,而且移动之量适与爱因斯坦的理论相符合。
其次,水星轨道每世纪有42角秒的差异,是牛顿的理论所不能解释的,但为爱因斯坦所阐明。他算得的数字为43角秒。
第三,按照相对性原理,原子在万有引力场内振荡应当较缓慢。平均说来,太阳光谱中的谱线,由于太阳上的重力较强,与地上相当光谱的谱线相比,应该向红色一端移位。这个预期的移位很难查出,但是实验数据的比较。表示其确实存在。在密度大的恒星的光谱内这种位移较大,有人已经在假定其为真确的前提下,应用这一学说来测量恒星的密度。
由此可见,要想作精密的计算,牛顿的理论是不及爱因斯坦的理论的。在量子论与相对论两个方向上,现代物理学似乎正在摆脱伽利略时代以来一向指导物理学而卓有成就的基本概念。新的思想须有新的工具去表达。在某些方面,事情已经很清楚,领导现代科学经过两个光荣世纪的牛顿动力学,已经证明不足以担负现今知识所赋予的任务了。就连原来是古典力学基础的物质的概念,至今也归于消失。所谓物质占有空间而历时不灭的基本观念,今已失其意义,因为空间和时间既非绝对的,亦非实在的了。现今所谓物质,只是时-空中发生的一串事件,以未知的而或有因果关系的方式相联系。由此可知,相对论已加强了最新原子理论所得的结果。牛顿的动力学仍能预测物理现象至高度的精确,仍能解决天文学家、物理学家与工程师的实际问题,但作为最终的物理概念,他的理论只留其荣誉于历史中了。
从广义相对论推导自然定律的最好方法或许就是1915年希尔伯特(Hilbert)所应用的最小原理。亚历山大里亚的希罗曾发现反射光所走的路线,常使其所经行的总距离为最小值。十七世纪费马把这一原理发展成为一个普遍性的原理——最短时间原理。百年以后,莫佩屠斯、欧勒与拉格朗日又把它发展为动力学的最小作用原理,而哈密顿于1834年表明,一切万有引力的、动力学的和电的定律都可以表达为最小值的问题。希尔伯特证明:按照相对论原理,万有引力的作用在于使时-空的总曲率成为最小值,或如惠特克(Whittaker)所说:“万有引力不过是代表宇宙要伸直自己的一种连续努力而已。”
广义相对论马上就废弃了由万有引力而生机械力的观念,重力成为时-空的一种度规性质。但是带电或磁化的物体仍然必须看做是受了力的作用。韦耳(Weyl)等人曾企图把电磁体纳入广义相对论理论中,但未完全成功。1929年,爱因斯坦宣布,他研究出一种新的统一力场理论。这种理论认为空间是一种介乎欧几里得空间和黎曼空间之间的东西,这样一来,电磁力也就成了时-空的一个度规性质。
1929年,爱丁顿宣布,他在另一个问题上把不同概念协调起来。电子的电荷e以hc/2xe2的组合形式出现在两个电子的波动方程式里,式内h为量子的作用量,c为光速。爱丁顿根据量子论与相对论算得这个组合式的数值为136,而根据米利根最近测得的e值,算得这个组合的值为137.1。这里的误差已超过实验的可几误差,但其近似也颇饶兴趣。的确,所有这一切现代的概念很有可能在一个新的物理的综合下统一起来。
物理学近况
本书第六章所叙述的热力学的基本原理引导汤姆生与焦耳对气体的自由膨胀进行实验,因而促成绝对温标与氢和氨的液化(234页)。以后的年代里,这些方法被应用到工艺上去,于是为工业提供大量的液态空气与其他液态气体,并使物理学家、化学家、工程师得到极低的温度。在大气压力下,氢的沸点为-252.5℃,氦的沸点为-268.7℃。这里可以有趣味地指出,1931-1933年间,卡皮查(P.L.Kapitza)为液化氢与氦设计了一种新型的绝热仪器。这是一种具有松弛活塞的往复机。气体在液态空气或氮里冷却,在机器内受到25-30个大气压,然后使其从活塞和圆筒之间的缝隙间逃逸出去。这样气体就得到进一步的冷却,终于为汤姆生-焦耳的方法所液化。利用现代仪器所造成的低温,离绝对零点还不到一度的几分之一。
泰勒(Geoffrey Taylor)爵士用数学方法与实验方法研究,而且接近于提出一种完善的理论。他的研究结果在很多方面可以应用于湍性流体在管道里的流动以及晶体的受范形变,在气象和航空上,用途尤广。
卡皮查于1924、1927年和以后的年代中,先在剑桥、后在莫斯科提出了一个测定金属的磁性和其他某些磁效应的新方法。这个方法的基本特点是在若干分之一秒的时间内,给绕在试件上的测试线圈通以强大电流,快速工作的目的是为了避免过热;在通电时间内,实验是依靠自动装置来进行的。起初,电源是用一组缓慢充电、快速放电的蓄电池;后来用一台2000千瓦的单相交流发电机,当发电机通过测试线圈短接时,电能量的供给是依靠储藏在发电机转子里的动能。当电动力等于零时,自动开关接通了电路;当电动力再一次等于零时,自动开关就将电路断开。这样一来,仅仅半周波交变电流起作用,作用时间大约为1/100秒。发电机的绕组经过特殊的设计,可以产生顶部平坦的电流脉冲波,因此在这很短的时间内,磁场几乎保持不变。磁场可以达到几十万高斯的程度。实验装置的造价很高,需要大规模工艺设备制造,需要建造特殊的实验室来安放它们。线圈和发电机相距20米,在短路冲击到来前,整个实验就结束了,而这种冲击以每秒2000-3000米的速度,通过地面传向实验装置。
卡皮查与斯金纳(H.W.B.Skinner)在第一个厂房用13万高斯的磁场研究了塞曼效应。卡皮查在第二个厂房测量了铋和黄金的晶体的电阻率。他们发现磁场的变化弱的是按平方律,强的是照线性律;在室温到液态空气温度之间的温度范围内测量了35个金属元素。1931-1933年间,利用卡皮查设计的液化氢和氦的新仪器,在相当大的温度范围内,测定了许多物质的磁化率。
本书376页介绍过热离子学的初期研究工作。理查森爵士首先详细地研究了电子在真空里从热体逃逸的现象,而且给以完整的说明。同时他在光致发射方面的研究也有助于解释物质与辐射间的相互作用。他也研究了和化学作用有关的电子发射,对于填补紫外光谱与X射线光谱之间的缺隙也有相当的贡献。最近理查森更应用新量子论去解决氢光谱和氢分子结构的问题。
人们为了研究现代物理学,发明了许多新仪器,这些新仪器也引出不少新的问题与其解答。在这些新仪器之中,我们必须提到电子显微镜。上面讲过,电子流在磁力作用下,离开其直线路径而偏折,正如光线为透镜所偏折一样。而且正象透镜可以借光线而形成一个放大的像一样,磁力也可以用来在照片底版上形成一个图案。因为与电子有关的波的波长是光波波长的百万分之一,所以这些波能够给微小的物体造成一个明晰的形象。例如病毒,已被拍照下来,还有人尝试把分子那样大小的结构,拍照下来。
电磁波的理论应归功于麦克斯韦(1870),电磁波的第一次发现归功于赫兹(1887)。电磁波在无线电报与电话上的使用靠了两种发明:(1)马可尼(Marconi)将天线用于发播和收集信号,并使足够的能量发生作用;(2)上述热离子管研究成果的应用。
赫兹和早期的实验者所用的电磁波是感应圈所发出的电振荡;这些电波因阻尼大,很快便消失了。但无线电波的传递需要连续而无阻尼的列波。如果将热的灯丝和电池的阴极联接,再使灯泡里的一个金属板和阳极联接,灯丝所发出的电子便会形成连续的阴电流,从灯丝传到金属板。可是将电极互易,使无显著的电流通过。可见热离子管可以用作整流器,使半波通过,半波受阻。如果用铁丝网作成栅极,放在热灯丝与板极之间,而且使其带阳电,它便加强电子的发射,因而增加了热离子流。但是,相反地,如使其带阴电,则会使热电子减少。当电位发生逆转时,电流往返振荡,于是交流便重合在直流上。将这些往返的振荡通过变压器的原电路,再从剧电路回去,给栅极以其固有的交流电位,这样便维持住仪器的作用。由此可见热离子管有两种用途,即发射稳定的无阻尼的列波,并于接收时起整流的作用。使这些调整后的电流产生每秒100至10,000次的断续,再使其经过电话机,便可发出一个相当于音频的声音,因而形成了无线电话。
从无线发射出去的能量,可以分为沿地面传播的地波和在地平线上空传播的天波。天波,保持其能量的距离比较其在空间自由传播时所可以预期的要大得多。电波之所以能在长距离上传递,是由于日光使地球高空大气电离,而成为了导体。这一部分大气叫做电离层,也叫做肯涅利-亥维赛层(Kennelly-Heaviside layer)。这个名称是按照首先发现它的两个人的名字命名的。电波进入这一导电区,受到反射与折射而回到地面,如果距离相当长,电波又由地面反回电离层,如是往返数次,好象在甬道里传达一般。靠了研究长距离无线电波的形态,获得许多关于电离层或多层电离层的知识。从事这一工作的先有阿普顿(Appleton)爵士与巴尼特(Barnet),后(1925)有美国的布赖特(Breit)与图夫(Tuve)。后两人使用的是短暂的脉冲波。1926年,阿普顿证明,高出地面150英里还有一个反射或折射层,比其他层的电性更强。这种反射使无线电波的行径发生弯曲,因而使环球传递成为可能。同一原理也应用于无线电定位,即现今所谓的雷达技术。
固体反射电波,因而在发射处产生回波。这一原理在战争时期有极大的价值,导至1939-1945年间雷达在各方面的惊人发展。
脉冲方法可用于大多数目的。一个电振荡器发出一个厘米波的猝发辐射,有时历时不过百万分之一秒,由磁控电子管供给以足够的能量。这种磁控电子管是伯明翰大学的一个工作组设计的一种装置。利用天线使能量集中于一个十分确定的波束里。这束波在空间搜索,正如探照灯之照亮远物一般,因而可以发现远处的船只、飞机、飞弹、地形,甚至即将来临的风暴中的雨点。回波被他拍接收机所捕获,而在阴极示波器上表现出来。
1940年,英国的雷达发现了敌人飞机的来袭,在不列颠战役中起了很大的作用,使少数人能够拯救很多人的生命,继后与美国合作,证明盟军的雷达的优越性,大有助于赢得最后的胜利。
海战与航海也因此发生了革命性的变化。由于雷达可以定出远处的船位,因而可以在敌舰还没有出现在视线内时便开始攻击。雷达不受黑暗的妨碍,它可以导引船只穿过雾气,安全入港,且可以导引飞机到达轰炸目标而又返回基地。
核型原子
上面说过,放射物质所发射出的带有阳电荷的质点在云室里的踪迹,通常都是直线的,但是偶尔也可以观察到方向的骤然改变。1911年,卢瑟福根据比较间接的测量导出这些罕见的偏折,因而他想象原子的中心有一个微小的阳电核,在碰撞时把a质点排斥出来。
起初原子被看做是一个行星系的结构,阴电子环绕核心,在牛顿式的轨道上运行。但是上面说过,量子论的创立与应用,在原子的概念上引起了一场革命。新理论的主要特点在上述的那个时期里已经建立。但是在以后的年代里又掀起另外一场观念上的革命,主要是由于发现了原子内新型粒子并且发现了产生、计数和使用它们的方法。
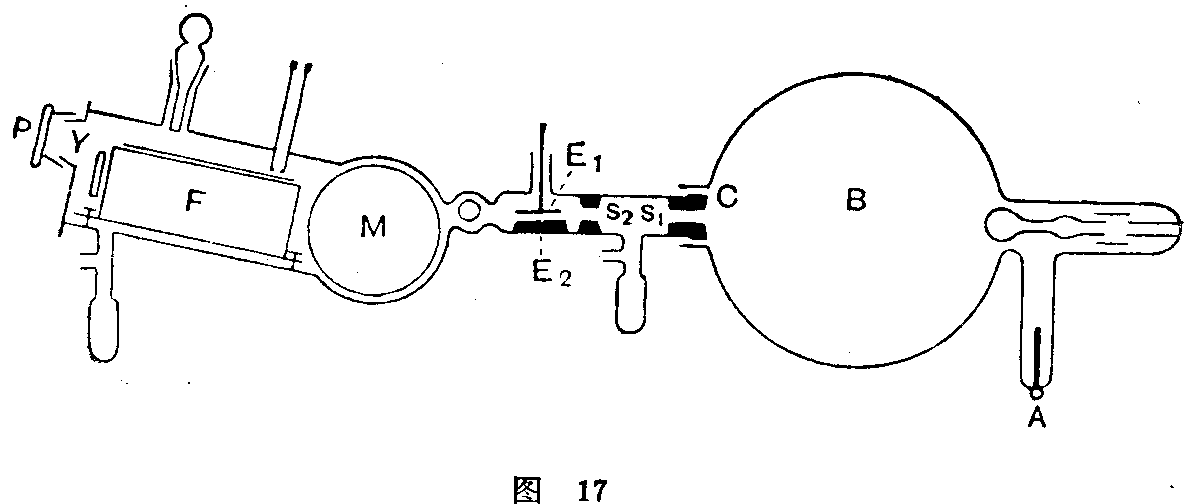
在叙述这些新的粒子以前,我们必须追溯一下阿斯顿等人在元素及其同位素的原子量的知识方面所取得的巨大进展。阿斯顿的质谱仪(第一部质谱仪规时陈列在南肯辛顿科学博物馆内),是根据J.J.汤姆生研究阳射线的仪器的原理制成的。玻璃球B(图17)为水银唧筒维持在低压下,其中盛有要研究的元素的挥发性化合物,或者是这种元素的卤盐所构成的阳极。阳极在A,阴极在C,其中穿有一隙缝S1。从阳极来的经过阴极隙缝的阳射线,再经过第二隙缝S2形成一个狭窄的阳射线束。这一窄束又经过两绝缘板E1和E2之间,这两极同200-500伏的电池组的两极联结,这样,这一射线束就展开成为一个电波谱。再利用两个光栏将这波谱的一部分隔离,然后使它在电磁铁M的两极之间经过。两个接地的铜版F保护这些射线,不受偶然的电场的影响,于是射线形成隙缝的聚焦像,而落在照相底片上。电磁力所造成的偏折,使速度不同而有相同的e/m(电荷-质量比)值的射线,聚焦在底片的同一点上。
如果取一条谱线作为已知,把它与未知电磁场里的其他谱线比较,便可测定原子射弹的相对质量。或者将磁场维持不变,调整电场,使未知谱线占据已知谱线先前所占的位置,也可以根据电场的强度算出相对质量。这两个方法均可以将已知和未知粒子的质量加以比较。这个仪器所给出的测量值仅仅取决于质量,所以叫做“质谱仪”是很恰当的。第一台仪器所测得的质量,误差为1/1000,第一台改进到1/10,0000芝加哥的登普斯特(Dempster)发明了另一种仪器,内有磁场使射线弯曲成半圆形。还有一种质谱仪是哈佛的班布里奇(Bainbridge)所设计的,可以用来进行很精密的测量。
1919年,阿斯顿的第一台质谱仪使用之后,研究成果纷至沓来。两条确定的谱线证实了汤姆生研究氖的结果,在某一时规里差不多每个星期都有新的同位素发现。1933年,阿斯顿在他的《质谱与同位素》(Mass Spectra and Isotopes)一书中说:“在一切已知有相当数量存在的元素里,现在只有18个还没有分析过”。到1935年,人们已经知道有250种稳定的同位素了。最复杂的元素好象是锡,它有11种同位素,其质量数目112至124。根据这些实验,普劳特首先提出的原子量是整数的规律,已经得到证实。210这个数字以下,差不多每一个数字都有一个稳定的基本原子。许多位置,两次或三次被某些同位素占去,它们叫做“同量异位素”,换句话说,即是重量相同而化学性质不同的原子。
如上所述,α和β粒子的性质已为卢瑟福早期关于放射现象的研究所肯定了。a粒子是氦原子核,根据阿斯顿的测量,它包含一个4.0029(氧取为16)的核质量和一个阳电荷+2e,即两倍于电子上的阴电荷-e。a粒子运动的速度在每秒2×109厘米或10,000英里左右。氢原子核或质子,包含1.0076的质量与一阳电荷+e。伯奇(Birge)指出,事实表明有氢的重同位素存在,同时吉奥克(Giauque)与约翰逊(Johnson),继后有梅克(Mecke),根据观察带状光谱的结果,取得质量为17与19的重氧存在的证据。
1932年尤雷(Urey)用分馏法发现氢的同位素,其质量为2,等于正常氢的两倍,在一般氢元素里仅占1/4000。这种重氢(2H)叫做“氘”(D)。如果使电荷从其中通过,有些原子失掉一个电子,而成为正离子,被人叫做“氘核”。它们好象是质子和中子联系在一起的结构。瓦什伯恩(Washburn)把普通水电离,得到一种新物质:重水,其中氢为其同位素氘所代替。重水为刘易斯所分出,密度比寻常水大11%,而其冰点与沸点也不相同。现在已能制造重水,中性氢(1H)的质量可以更准确地测定,其值为1.00812。
还有另外一些时常穿过大气而来、贯穿力更强的射线,可以在威尔逊云室内探测出来。它们的来源好象在宇宙空间里。这些年来有很多人去研究它们,特别是米利根和他的同事们。这问题可以说开始于1909年,起初是格克耳(Gockel),后来是海斯(Hess)与科赫斯特(Kolhorster),都发现验电器放在升空气球上,比在地面放电更快。这说明位置愈高,造成电离的射线愈多。1922年,包温(Bowen)与米利根将这些实验拿到55,000呎的高空去做,1925年米利根与卡梅伦(Cameron)将验电器逐渐下沉到70呎深的没有镜的水里而发现放电率连续减少。在以后的年份里,有些观测者走得更远。这些射线的贯穿力比地上任何射线都大。地磁对于这些射线的效应,说明其来源不在高层大气里。而且,这些射线的强度昼夜都是一样,因而它们不是从太阳而来的。当银河不在南半球的地平线上时,仍然有这些射线,因而它们的来源也不在我们的星系里,所以它们当是从银河系以外的天体或自由空间而来。
这些宇宙射线的能量可以根据其穿透力加以粗略估计。安德生(Carl Anderson)与米利根首先做了比较精确的测量。他们使宇宙线通过很强的磁场,而观测其偏折。能量在6O亿(6×10[9])电子伏特左右相当确定的范围内变化。安德生于1932年利用这仪器发现具有阴电子质量的阳性粒子。这种阳电子,早由狄拉克据理论预言其存在。这种粒子后来被命名为正电子。读者当记得,以前已知的最小的阳性粒子是氢原子的核(质子),其质量约2000倍于电子。正电子的发现又使我们对于物质的概念发生根本性的改变。
和其他带电粒子一样,正电子穿过物质时产生电磁波。宇宙线的频率比X和Y射线为高,其范围在每秒1022至1024周,而可见光的频率只有1014周。这些频率不是直接测定的,而是将能量除以普兰克常数h而算出的。
1923年,康普顿根据量子论,提出可以和电子与质子相比拟的辐射单位的概念,他将这个单位命名为光子。如果一个光子以足够的能量打击一个原子核,特别是重原子核,一对正-负电子同时出现于云室里。这是1933年布莱克特(Blackett)与奥基亚利尼(Occhialini)首先提出,不久即为安德生所证实的。这类成对的电子的动能约为160万电子伏特,而入射光子的能量为260万电子伏特。这100万电子伏特的差数可以量度电子对的“固有能量”,是具有辐射能量的光子的物质化,这表现辐射转化为物质。反之,假设正负电子互相湮灭,就有两个电磁辐射的光子,每个的能量为50万电子伏特,从相反的两个方向射出。这个设想于1933年经提博(Thibaud)与约里奥(Joliot)由实验加以证实。
在海平面处已经发现具有三、四十亿(109)电子伏特的宇宙线。它们常以簇射(阵雨)的形式出现。在14,000呎高的尖峰山(Pike’sPeak),这现象尤其常见。根据贝特一海特勒(Bethe-Heitler)的簇射形成理论,一个入射高能电子先将其能量转化为“冲击光子”,这光子产生电子对,每个电子重演这一过程,直到所有的能量一律降低,成为低能的光子与电子。从地球外面来的正射线可能不会达到海平面,至于在云室里所观测到的高能正负射线,可能是在大气里形成的次级宇宙线。1934年,安德生与尼特迈耶尔(Neddermeyer)假设具有高度贯穿力的踪迹是质量在电子与质子之间的粒子的踪迹,这种粒子经安德生命名为“介子”。这两位物理学家于1938年证实了他们的假设,测量得这些粒子的质量为电子质量的220倍,1939年别的观测者又量得为200倍,而质子的质量约为2,000倍。由此可见,要说明物质的结构,需要一个多么复杂的图案!
在大多数的情形中,宇宙线里的粒子多是电子而很少质子。这表示宇宙线在进入太阳系以前不可能穿过很多物质;这样它们的来源好象不可能在银河系里的恒星上,而必须在银河系外的空间。
宇宙线的成因与来源仍然是一个只能猜度的谜。人们提出的假设有如下几种:(1)电子经过某一天空静电场降落而形成说,(2)经过双星磁场形成说,(3)按照爱因斯坦方程式mc2=E,物质质量一部或全部转化为宇宙辐射说。蕴藏量最丰富的元素可能释放的能量由110至280亿(1.1至2.8×1010)电子伏特,一半射向一方,另一半射向反对方向。所以一半所给出的能量在5至14×109电子伏特之间,观测所得的数值大致也是这样。
上面讲过,1919年卢瑟福发现,用a粒子轰击某些元素,例如氮,引起原子的变化,因而发射出运动迅速的氢原子核(质子)。这发现不久即为布莱克特所证实。他在威尔逊云室里拍照了质子的踪迹。这发现是在受控原子变化实验方面取得巨大进展的起点。这些受控原子变化实验取得了惊人的成果。当波特(BO比)使质量为9的铍元素受到这样的轰击时,他得到一种贯穿力比铀射出的最硬的Y射线还强的新辐射。1932年,查德威克(James Chadwick)爵士证明这种辐射的主要部分不是Y型的射线,而是一些运动急速不负电荷的粒子流,其质量大约与氢原子相等。取得这些粒子的方便办法就是,将几毫克的铀盐与粉末铁混合,而封闭在一管内,这种粒子即从管壁逸出。由于这些粒子不负有电荷,因而称为中子,在其行程里,它们可以自由地通过原子,而不造成电离。
下表列举了1944年已知的粒子,无疑以后还有更多的发现:
| 名称 | 质量(单位:电子) | 电荷 |
| 电子(β粒子) | 1 | -e |
| 正电子 | 1 | +e |
| 介子 | 200 | ±e |
| 质子 | 1800 | +e |
| 中子 | 1800 | 0 |
| 氘核 | 3600 | +e |
| α粒子 | 7200 | +2e |
除了这些算作物质的粒子之外,还有作为辐射单元的光子。宇宙真是复杂而神秘。
费瑟、哈金斯(Harbins)与费米(Fermi)证明中子,特别是慢中子,虽然不能引起电离化,但却可以十分有效地促进原子核变化。它们不象a粒子那样受带正电荷的原子核的排斥,因而容易进入较密的原子核,而改变其性质。例如使用渗透有锂盐的底片进行实验时,在显微镜里便可看见相反的两个踪迹。使用硼,特别是用一种铀的轻的同位素,也可发现类似的变化。
居里-约里奥夫妇用a射线直接轰击这些轻粒子,得到一些新的放射物质。例如硼受了a射线轰击一会之后,便发出正电子流。其放射性的衰变和正常的放射性相似,是时间的几何级数,在11分钟内衰减一半。这种植变可以下列化学方程式表示:
10B+4He→14N→13N+中子。
氦核14N因具有过多能量,是不稳定的,于是分裂为比较稳定的13N与中子。然后13N更缓缓地转变为稳定的碳原子与正电子:
13N→13C+Σ+。这种放射性的氦可以作为具有氦的化学性质的放时气体收集起来。
人们已经利用a射线、速质子,特别是慢中子使很多种物质变成放射物质,其中慢中子就是对于最重的元素也是有效的。以上只叙述了用直接间接由放射物质得来的各种粒子轰击元素而造成元素的受控嬗变的情况。这样直接间接由放射物质得来的粒子为数不多,因此多年来物理学家希望发明人工制造有效的强粒子流。后来这种希望是实现了。
在氢或其同位素氘里放电,可以得到大量的质子与氘核,但要使它们达到造成嬗变所必需的高速度,必须在很强的磁场里把它们加速。要取得高达百万伏特的高电压,便需要大型的工艺装置,并需用现代的高速唧筒,以维持高度的真空。
科克拉夫特(Cockcroft)与瓦耳顿(Walton)在剑桥进行的实验是这方面的开路先锋。他们利用一套电容器与整流器将变压器的电压增高,现在所期望的是用大型装置取得具有200万伏特电压的直流电,它能产生长20呎的火花。还有一种静电装置是华盛顿的范·德·格拉夫(Van de Graaff)所设计制造的,这装置内有一传输器,不断地将电荷送入一个中空金属绝缘球去,以致达到500万伏特的高电位。
加利福尼亚的劳伦斯(E.Lawrence)教授发明一种加速器,名叫“回旋加速器”,离子在这装置里经过一个交流电场,和与之正交的磁场。这个装置使质子和氘核循半径递增的螺旋形的路径而运动,间续地进出于电场。为了达到交流电位的某一特定频率,离子总是在电力处在可以把离子进一步加速的运动方向上的时候进入电场。这样,劳伦斯得到了质子和氘核的强粒子流,其能量高达1600万伏特,而具有100微安的电流。这样获得的效果等于16公斤的纯镭所射出的α粒子。
这一类的装置无异是将极强有力的武器放在实验者的手里。科克罗夫特与瓦耳顿证明,可以用大约十万伏特的质子,使锂与硼产生人工的嬗变。从这种电压以至回旋加速器的几百万伏特,现代的实验室现在有了一系列能量范围很广的可以引起嬗变的射弹。
锂有质量为6和7的两种同位素。在质子的轰击下,有时一个质子进入7Li的梭。这样产生的8Be不稳定,立即分裂为两个快速的a粒子,即氦核,循相反方向射出。如果用氘核代替质子去作射弹,6Li捕获一个氘核之后,又产生一个8Be的核,但具有大量的剩余能量。这种8Be的核也象前一个反应一样,分为两个a粒子,但具有比质子进入7Li而产生的a粒子有更大的速度。7Li捕获一个氘核之后形成9Be,再立刻分裂为两个α粒子和一个中子。
这些不过是奥利芬特(Oliphant)和哈特克(Harteck)首先加以研究的嬗变的几个例子。仅借两万伏特就可以引起这种嬗变,来加速氘核射弹。以后还研究出许多复杂得多的变化。从实验获得许多新同位素,如质量为3的氢(3H),质量为3的氦氨(3He)。根据其释放的能量,可以算出这两种同位素的质量:
2H +2H =1H +3H+E
2.0147+2.0147=1.0081+2H+0.0042
氢和氘的原子量就是阿斯顿用质谱仪算出的数值。至于上式中所释放的能量E值是根据观测质子在空气中的行程(14.70厘米)而算出的这种行程说明质子的能量为298万伏特。释放出的能量的3/4应归于质子的动能,因而E的总值为397万伏特。根据爱因斯坦的理论,质量与能量是等价的;质量减少dm相当于释放c2dm的能量(这里c表光速,以每秒厘米数计为3×10[10]),所以与397万伏特相当的质量为0.0042,因而3H的质量为3.0171。
劳伦斯和他的同事们利用在回旋加速器里形成的、能量为1600万伏特的高速氘核去轰击铋,把它转变为放射性同位素,同天然放射性产品镭E相同。这是一个很有兴趣的成果。同样质量为23的钠或钠盐被高速氘核所轰击,产生质量为24的放射性同位素。这种放射性的钠分裂时,发出一个β粒子,而形成质量为24的镁的稳定核,其半衰期为15小时。因此劳伦斯得到强的放射纳的源,可以作为镭的代用品,用于医疗工作。
查德威克与戈德哈伯(Goldhaber)使用γ射线将氘核2D分裂为质子与中子。齐拉德(Szilard)将质量为9的铁(9Be)分裂为8Be与一个中子。这一方法能否发展;取决于能否取得高能强γ射线。
在这一时期里得到250多种新的放射性物质。这些不稳定的同位素可能存在于太阳上,也可能存在于刚从太阳分出的地球上,但是随着地球变冷,它们便消失了,只留下衰变期很长的铀和钍了。
这些人工变化里,有些能量变化甚至比天然放射性分裂中的能量变化还要大。例如21,000伏特的氘核可以使一个锂原子变化,而发出2250万伏特的能量。因此可以赢得大量的能量,初看起来好象可以在这里得到原子能的无限源泉。可是在一亿(108)个氘核中大约只有一个可以发挥作用。所以出入相抵,我们所要供给的能量超过所获得的能量。而且就中子而论,中子自身只能用效率极低的方法获得。在1937年,的确,看起来好象用人工改变的方法从原子中获得有用能量,并没有多大希望。在这一点上,我们应当记得,在应用科学的历史上,以前希望没有这样大的前景,都曾经使得宗教界的先知们惊恐万状过。事实上,1939年哈恩(Hahn)和迈特纳(Meitner)就发现当铀原子被中子撞击时,它的核分裂为两个主要成分,各占其质量的一半左右,而且出现二、三或四个中子。乍一看来,这好象就是我们要寻找的垒集过程,但事实上只有一种铀的轻的同位素(其原子量为235而不是238)可以分解到有用的程度,可是只有微量的存在。首先发现质量为235的铀的是登普斯特,明尼苏达的尼尔(Nier)和纽约哥伦比亚的布思(Booth),邓宁(Dunning)与格罗斯(Grosse)旋即研究了它的分解。同样的过程也发生于钍。那时许多实验室异常努力地从事这些同位素的分离。虽然困难很大,但是由于战争的刺激,很快就把这个工作推向高潮。起初轻的铀235须从成分很大的U238分出,或用小孔弥散法,或用阿斯顿的质谱仪法。分量少时,由于中子的逃逸,不能引起连锁反应,因而这物质是稳定而无害的。可是如果将无害的两块物质放在一起,而超过一定的份量,分解就逐渐垒集起来,并引起巨大的爆炸。
化学反应是由原子外围的电子的变化引起的,这种爆炸却是由于原子核的破裂所致,自然是一件可怕得多的事情。一磅铀所发出的核能等于很多吨煤燃烧时产生的热能量。
原子量为238的铀可用以捕获中等能量的中子,而发射出电子。这个过程形成一种以前未知的元素,被命名为钚(Pu)。
为了和平的目的,可能需要用“缓和剂”来吸收一些在核反应中释放出来的中子,借以控制而且减缓核反应。有些轻的原子,如石墨形态的碳,及前面说过的重水里氢的同位素,都可用作缓和剂。铀238可以插入缓和剂的“堆”中,所释放出来的热能可以用来发电。
在1939-45的战争期间,美英两国的物理学家、化学家与工程师,群策群力,共同合作,在制造原子弹方面和德国人展开了生死攸关的竞赛,并且在这一竞赛中取得了胜利。庞大而复杂的原子工厂在美国一个空旷地区建立起来,1945年投在日本的两颗原子弹结束了战争。留给各国政治家的工作便是控制核能的使用,以期使它为人类造福而不是造祸。我们面前摆着可怕的危险,也许核能的威力会使各国恐惧,从而迫使各国走上和平的道路。战争的消除当是科学的最大胜利。
同时原子研究的和平应用,已经为戴尔爵士等人所开始了。一个最显著的例子便是所谓“示踪元素”的使用。靠观测这类元素的性质,可以查明它们存在与运动的踪迹,其中最好的也许是某些放射物质。现今已有数量多得多的同位素作为原子堆的副产物,供入使用,因此在近年内示踪元素的应用发展异常迅速。放射原子可以混合在有机物内,作为动物的饲料,这样食物在体内的运动,可以用盖格-弥勒计数器去追踪它。我们可以不夸大地说,放射性示踪元素为生物物理学与生物化学打开了一个完全新颖的领域,且给予医疗界一个新的诊断法。
还有,放射物质的大量生产已经使放射治疗变得更容易、更便宜了,例如用以毁灭癌性组织。
还可以把示踪剂混在肥料里,靠估计农作物内的放射性,来测量肥料在农业生产上的效果。总之,示踪元素用途之广,差不多可以说是无限的。
物理理论的新发展,通常总是使人们要找到描述现象的数学方程式,比从物理学上加以解释,要容易。例如海森堡与薛定谔的量子力学,通过解决简单的例子建立起普遍的数学公式,后来才提出一些物理学的解释,例如状态的叠加和测不准原理,也导致了一种满意的非相对论的量子论。
要使量子论成为相对论性的,狄拉克也觉得解决数学方面的问题很容易,可是在解释上却有困难。他的解释最好用初始的与过渡的机遇来表示。这样,物理学如往常一样,仍然停留在概率演算的领域。
爱丁顿在我们所期待的物理学的新综合方面,取得一些进展。由于他把物理常数,如质子与电子的质量以及它们的电荷等等的理论数值与观测的数值加以比较,而得到很显著的符合,他成功地把万有引力、电力和量子论联系起来。关于现代物理学这方面的问题,可参看弗伦克尔(J.Frenkel)的一篇综合叙述。
化学
化学变化的动力学,在现代是一个不断研究的主题。阿累利乌斯首先提出:在一定量的物质里,只有一定数目的分子参与化学变化,而且这数目是随温度而增加的。这一理论现在看来是可疑的。现在人们以为这些分子,是由于“碰撞”,才变得运动迅速,从而起活化作用,就是在单分子的反应中也是如此。
氨与硝酸盐是农业肥料所需要的。硝酸盐也是制造开矿用的炸药和军用炸药所必需的。有一个时期,大家害怕(特别是克鲁克斯)智利的硝酸盐矿用完后,化学肥料会变得不足,世界小麦的供应也会变得不足。我们看见只有在战争时期才发生过这个现象。在正常和平时期是没有这个现象的。植物育种者已经培养出小麦的变种,可以适应北方的寒冷区域,因而扩大了种植面积,化学家也用合成方法制出了氨与硝酸盐。
卡文迪什曾将电火花在空气里通过,而得到酸。一百年后挪威的伯克兰(Birkeland)与艾德(Eyde)把这一方法加以大规模的发展。奈恩斯特(Nernst)与约斯特(Jost),继后,哈伯(Haber)与勒·罗西诺尔(Le Rossignol)研究了氨、氮和氢在各种温度与压力下的平衡,并且利用各种催化剂的帮助,于1905年前后研究出一种实验室方法,从空气制成了氨,而且到1912年,哈伯的方法已经在工业和军事的用途上取得了成就。这是由于在1914-1918年的战争期间受了德国需要硝酸盐的巨大刺激的缘故。这个方法就是使氮与氢在200或更高的大气压与500℃的温度下,在一种催化剂上面流动。再使氨与硫酸或硫酸钙起作用,而变成了硫酸氨,或将加热的氨和空气一道通过象铂绒那样的催化剂,使氨变成硝酸氨。
一百多年前开始研究的一些催化剂,现在对于化学的动力理论与许多化学工业,起了很重要的作用。催化剂很久以来就用于象哈伯法那样的反应中,近年来应用得更广。将氢气通过混有镍屑的热油液,油便氢化,而变成一种熔点较高更可口的脂肪。在高压下使氢气通过碳粉与煤焦油混合的热糊剂,并用一种适当的催化剂,可使其氢化。生成物经过蒸馏,便成为汽车用的轻油、中油和重油。催化剂用途的例子,多至难以一一列举。
莫斯利的元素表中的缺空,现在已经差不多填满了。1925年,W.和I.诺达克(Nodack)使用X射线分析,发现了43和75号元素,而命名为锝与铼。1926年B.S.霍普金斯(Hopkins)宣布他发现了61号元素仅(Ⅱ即钷Pm)。这或许还没有得到完全的证实、周期表上的倒数第二个缺空——一个元素属典类名成(At)——于1940年由加利福尼亚大学的科森(Corson)、麦肯齐(Mackenzie)与西格雷(Segre)发现。他们在回旋加速器里,用a质点轰击铋而发现这个元素。
卢瑟福-玻尔的原子理论,经过修改以后,使我们对于化学结构有了一个电子的概念。电子可以占据的轨道或能级,由主量子数n=1,2,3等等规定,这也表示壳层里的电子的数目。这些能级上可以存在的最多的电子数是由下列级数(里德堡级数)给出:2×12,2×22,2×32等,外层最多的电子数是8。一满了8这个数,使特别稳定;这种情况发生在除氦以外的一切惰气中;在n=1时,氦有两个核外电子,而氢只有一个。到了钠,开始形成量子数为3的另一个新的电子壳层,到了氩而满额。氢的电子结构是2,8,8。
这一理论给原子价的学说提供了物理学的根据。化合可以看做是电子从一个原子迁移到另一个原子去。原子价代表一个原子必须获得或放弃的电子数。这个原子必须获得或放弃这么多的电子,才能形成一个电子结构同最邻近的惰气一样的体系,或者说形成具有8个电子壳层的体系。化合也可以由于两原子共用一些电子而发生;这种原子价叫做共价。牛津的西奇威克(N.V.Sidgwick)对这一原子价理论阐释得特别详细。
如果两个原子的轨道共用两个电子,它们便是靠所谓共价键结合起来的。如果两个电子不是均等地共有,则一个原子具有多余的阳电,另一个具有多余的阴电。这个分子将具有极性,并且具有偶极矩,这等于一个电荷同两电荷之间的距离的乘积。这些极矩可以根据介电常数(电容率)或不均匀磁场里磁束的偏折度估算出来。雷德(Wrede)、德拜,还有西奇威克与包温,都对偶极矩进行过研究,以此作为探索化学结构的指针。单质分子如H2、O2没有偶极矩,因此是均等地共有电子,但是HCI有一极矩,为1.03×10-18静电单位,原子间的距离是1.28埃;其他化合物也是这样的。
波动力学在化学上也如在物理学上有其重要性,特别表现在共振原理上。共振的发生是由于一个分子由一电子结构跑到另一电子结构中,并且表现出两者的某些性质。
原子发射出线状光谱,但从分子可以得到带状光谱,其分子的组态也可以测定出来。一束单色光经过透明物体时发生散射,由此而形成各种频率的辐射——散射介质的特征(斯梅卡耳-拉曼效应)。哈特利(W.N.Hartley)等人新近证明,结构相似的化合物在紫外区有相似的吸收光谱。他们还从分子结构的观点,研究了红外吸收光谱。
劳厄首先提出用X射线考察晶体结构,先后有弗里德里希与基平,布拉格父子(384页)加以研究。这种研究表明,氯化钠的立方晶体由钠离子组成。每个钠离子为六个氯离子所包围,相同地每个氯离子也为六个钠离子所包围。金刚石里每个碳原子都处在四面体的中心,而与角上的四个碳原子互相束缚。这种紧密的结构说明金刚石的硬性。用X射线对二苯基晶体的分析表明,它具有六个碳原子组成的环形结构,和凯库勒由苯与其衍生物的化学现象推断的一样。新近罗伯森(J.M.Robertson)等人将傅立叶级数的方法应用于萘与蒽,以测定许多化合物组成原子的排列方向和化学键的性质。X射线也被用于考察合金、无机与有机化合物,都有成就。
对于晶体结构的分析,不但可以利用X射线进行,也可利用电子衍射进行,因为以上讲过,运动的电子挟带有波列,而可表现干涉现象等等。由电子衍射和X射线所得的结果是相合的。德拜使用X射线研究晶体粉末,后来发现用相似的方法,对液体与气体也可以得到干涉花样,并且可以测定原子之间的距离。1930年,维耳(Wierl)更使用了改进的方法。
凯库勒发现的苯的环形结构式以及范特-霍夫和勒·贝尔的碳原子结构成四面体的理论,成为立体化学的伟大结构的基础。如果承认碳原子的四个价电子作四面体的排列,则价电子键之间的角度将是109度28’。如果形成环状,由于正五角形的角为108度,一列五个碳原子,首尾两端必然互相接近,形成环状,键间很少应变,因而很稳定。W.H.珀金(Perkin)(子)制出了具有3、4、5和6个碳原子的环状的化合物,近年来,化学家,特别是索普(Thorpe)与英文尔德(Ingold)等人证明,从一个碳原子出来的两个价电子之间的天然角度,显著地受到所附的基团(如甲基团)的影响,因而应变可以减少,稳度可以增加。这种环结构出现在许多天然物里。如范特-霍夫所预测的,旋光性出现于不对称的分子,可是却没有不对称的碳原子。梅特兰(Maitland)和米尔斯(Mills)已经证明丙二烯型化合物的情况就是这样,它们的分子并不具有对称面。化学这一分科的大发展是靠了X射线分析的应用,因为这种分析将原子和分子的结构,表现得异常明白。
建立在煤焦油基础上的化学工业,范围极其广阔。它从理论科学产生,而反转来对理论科学有很大的影响。翁韦多本(Unver-dorben)与霍夫曼(Hofmann)从煤焦油分离出一种名叫苯胺(安尼林油)的物质。霍夫曼还证明煤焦油里有苯。W.N.珀金(父)于1856年用重铬酸钾处理硫酸苯胺,而得到紫色或紫红色的安尼林;这是首创的安尼林染料,以后发明了很多种这类染料。1878年,在库珀(Coupef)和凯库勒奠定的基础上,E.和O.费舍(Fischef)首先阐明了它们的化学结构。他们证明玫瑰苯胺(一品红)、洋红等的来源是碳氢化合物,三苯甲烷。这工作引出许多新染料和合成这种染料所必需的中间体。后来格里斯(Griess)制成具有偶氮基团(N:N)的偶氯化合物。这又导出一个新系的偶氮染料。
茜素染料,如土耳其红,于1868年合成,跟着而来的有蒽醌的其他衍生物。约在1897年,从苯基甘氨酸制出的工业蓝靛,开始将天然蓝靛逐出市场,使印度的种植者破产。
染料在工业上虽属重要,药物对于人们的福利更有贡献。有机药物的合成时代开始于解热药,如安替比林(1883),止痛剂非那西汀(1887)与水杨酸,即阿斯匹灵(1899)。这些药物的发现,创立了现代的化学治疗学硕,主要的创始人当推欧立希(Paul Ehrlich,1854-1915年)。他制成一种医治马病的药物与一种名叫盐酸二氨基联砷酚(即六①六)的砷化合物,能杀灭在人体内造成梅毒的螺旋体菌(1912)。尿素的一种复杂衍生物,于1924年为富尔诺(Four-neau)所制成,能消灭造成昏睡病的寄生虫。以后几年,一系列以氨苯磺胺和磺胺吡啶等磺胺类药物为基础的合成药,由梅(May)与贝克(Baker)合成,叫做M.B.693,对于控制伤害人畜引起很多疾病的链球菌和肺炎球菌都很有效,而磺胺胍成了痢疾的特效药。
起初这些药物并无理论的基础,到1940年菲尔兹(FildeS)、伍兹(Woods)与塞尔比(Selbie)才证明,磺胺类药物的作用在于阻止病原菌获得它们生长所必需的另一种同族物质,名叫对氨基苯甲酸。这个成就表明进一步探讨的方向应当是研究细菌的代谢,寻找细菌所需要的物质,并找出防止细菌利用它们的方法。
青霉素最初是由弗莱明(A.Fleming)爵士在1929年从笔毫霉制出并命名的,后经牛津的弗洛里(Florey)等人加以研究,并证明比磺胺类药物更有效。
在帝国化学工业的曼彻斯特实验室里,于1945年发现一种抗疟疾的特效药名“白乐君”(Paludrine)。杀虫药也经人研究,一种能杀昆虫而于人畜无害,名叫六氯化苯(即六六六)的杀虫药制备成功了。
维生素的最新研究成果要在生物化学栏内作总的叙述,但关于维生素的结构与合成的叙述,很自然地要放在化学栏里来。维生素A是生长必需物,其成分为C20H30O,卡勒(Karrer)提出了一个结构式,说明它的化学反应及其与它的前身胡萝卜色素的关系。维生素B1,有抗神经炎的功能,为哥伦比亚大学的威廉斯(Williams)所合成。抗坏血病的维生素C,存在于绿色菜蔬与柑属水果里,其结构式比较简单,表示如图18。这种维生素先经人提取,后于1933年为伯明翰的霍沃思(Haworth)合成,现在称为抗坏血酸。
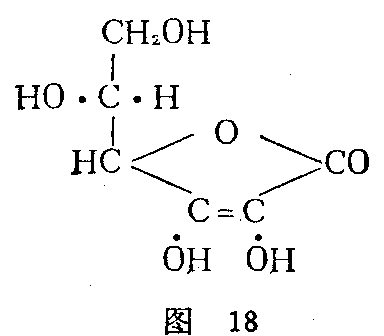
以上讲过,有机化学的基础在于碳原子具有互相结合为复杂结构的能力。大致类似的能力也为硅所具有,近年来也变得很重要。
1872年,冯·拜尔(Von Baeyer)发现酚(石炭酸)与甲醛化合成为一种树脂物。1908年,贝克兰(Baekeland)发现这种树脂在碱性的催化剂内加热,变成一种有塑性的物质。这叫做“电木”,在以甲醛为基本材料的反应中还取得了其他塑料物。它们可以用作漆料、釉料,并可用来制造留声机唱片、飞机骨架等。
橡胶于1892年由蒂尔登(Tilden)用异甲基丁二烯合成。1910年,马修斯(Matthews)发现金属纳可以促进异甲基丁二烯的聚合化,但现今异甲基丁二烯已经由碳氢化合物,丁二烯或氯丁二烯取代了。这些合成物常加在天然产品内。
合成有机化学家对照相术作出了很多的贡献。起初,他们制成了显影剂(焦性没食子酸等),继后制成一些染料,这些染料使胶卷对光谱可见区与不可见区的不同的光线都具有感光作用。由于制出对于红外光具有感光作用的照相乳胶,几哩以外的对象,也可摄得清晰的形象,这用普通底片是办不到的。照相术对于许多学科,自天文学以至微生物学都很有帮助。
费舍对于单醣的基础研究工作(253页),为许多人所继续,他提出一个敞开的链形结构式,不过,人们现在公认的是霍沃思所提出的六成分型环形结构式。伊尔文(Irvine)与霍沃思和美国的赫德森(Hudson)使用甲醚研究象蔗糖那样的双糖。开始了氨基酸的现代研究的也是费舍。但迄今为止用合成方法制出的结构最复杂的多肽类合成物,虽然分子量超过1300,还是离蛋白质很远。蛋白质可以分为两类,其分子量分别为35,000与400,000的简单倍数。现在虽然通过动物纤维的X射线研究,得到了蛋白质分子结构的形象,但仍有相当距离,人们还不能合成蛋白质。
现代的物理与化学仪器,比五十年前的复杂得多了。个人很少能够建立起一个实验室。业余爱好者虽然在过去对于科学作出了不少的贡献,但他们的时代似乎过去了。现在大多数文明国家的政府都资助研究工作。英国将补助费送给各大学和皇家学会去进行基础研究工作,至于工艺的研究则交给科学与工业研究部、医学研究理事会或农业研究理事会去掌管。
------------------
素心学苑 收集整理
前一页
回目录